这里简单介绍一下立体角的概念。
定义
在考虑辐射传输问题时,为了度量源点对某一范围的视场角大小,我们引入立体角的概念。通常教材上的定义如下图所示,一个半径为 $r$ 的球体,用顶点与球心重合的圆锥去截球面,截取的球面积 $A$ 的大小除以半径的平方,即是立体角。
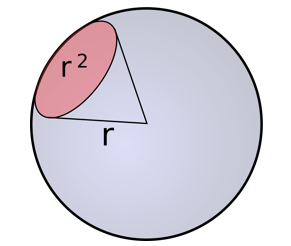
公式为 $$ \Omega = \frac{A}{r^2} $$ 立体角的单位是无量纲的球面度(steradian),简写为 sr。实际上,除了用圆锥,你用任何几何体去截都行,只要能在球面上划分一块连续的区域,其面积为 $A$,那么便可以通过上面的定义式计算出其立体角。
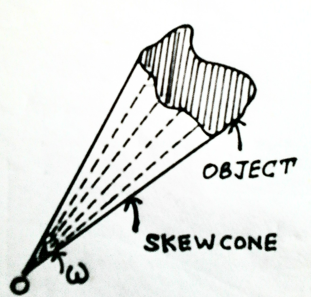
关键在于,立体角的本质是一段封闭曲线对于观察点所张开的角度,只有这个角度是重要的,毕竟我们引入立体角就是为了获得这个视场角。而封闭曲线围成的曲面具体是什么形状,其实并不重要。就如同下图所示。
于是,为了从球面立体角的定义式出发计算任意曲面的立体角,把曲面的面微元都投影到以矢径为半径的球面上,投影面积除以矢径长度的平方后,再做面积分,式子为 $$ \Omega = \iint_S \frac{\vec{e_r} \cdot d\vec{S}}{r^2} $$ 其中 $r$ 为观察点到曲面上一点的距离,$\vec{e_r}$ 为矢径 $\vec{r}$ 的单位矢量,$d\vec{S}$ 为曲面 $S$ 上法向的微元面积,$\vec{e_r} \cdot d\vec{S}$ 即意味着把面积微元投影到球面上,于是根据球面的面积微元表达式,得到立体角的微元表达式 $$ d\Omega = \frac{\vec{e_r} \cdot d\vec{S}}{r^2} = \frac{dS_0}{r^2} = \frac{r^2 sin\theta d\theta d\varphi}{r^2} = sin\theta d\theta d\varphi $$ 其中 $\theta$ 为天顶角,$\varphi$ 为方位角。从这个表达式可以看出,立体角的大小与 $r$ 无关,而只与曲面张成的角度(即 $\theta$ 和 $\varphi$ 的范围)有关,也就是说,给定一个角度张成的锥体,其中截取的任意形状、任意距离的曲面的空间角都相等。若观察点被封闭曲面包围,对全空间积分,很容易得到 $$ \Omega = \iint d\Omega = \int_{0}^{2\pi} \int_{0}^{\pi} sin\theta d\theta d\varphi = 4\pi $$ 即封闭曲面内任一点所张成的立体角的大小为 $4\pi$。这一结果还可以从球面的例子来验证,球面面积为 $4\pi r^2$,除以 $r^2$ 后得球心处的立体角为 $4\pi$。
有这样的可能,曲面对于 $\vec{r}$ 来说不是单值的,即曲面在空间中绕来绕去发生了重叠。此时立体角的公式依然成立,因为一旦曲面发生重叠,立体角锥一定会穿过曲面三次,其中两次计算的立体角由于投影面积的方向性会抵消,只剩下穿过一次的结果。这种情况的证明可见于电磁学教材上(虽然这种情况我们也完全不用管就是了)。
一个例子:两个相隔较远物体互相张成的立体角
两个任意形状的几何体 $A$ 和 $B$,相距为 $R$。图示如下
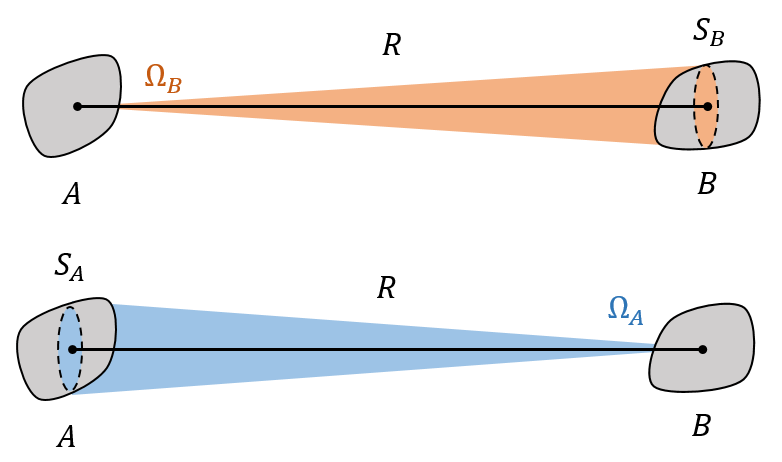
设物体 $B$ 对 物体 $A$ 中心张成的立体角为 $\Omega_B$,物体 $A$ 对 物体 $B$ 中心张成的立体角为 $\Omega_A$。这个张角的范围是从一个物体中心向另一个物体表面做切线得到的。根据定义式,有 $$ \Omega = \iint_S \frac{\vec{e_r} \cdot d\vec{S}}{r^2} $$ $\vec{r}$ 为物体中心到另一个物体表面的矢径。当两个物体相隔很远,$R$ 远大于它们自身的长度尺度时,$\vec{r}$ 的长度变动很小,长度近似等于 $R$ ,其方向变动也很小,方向近似不变,与两物体中心连线平行。这一近似可以用照射到地球的太阳光近乎平行的事实来说明。如下图所示
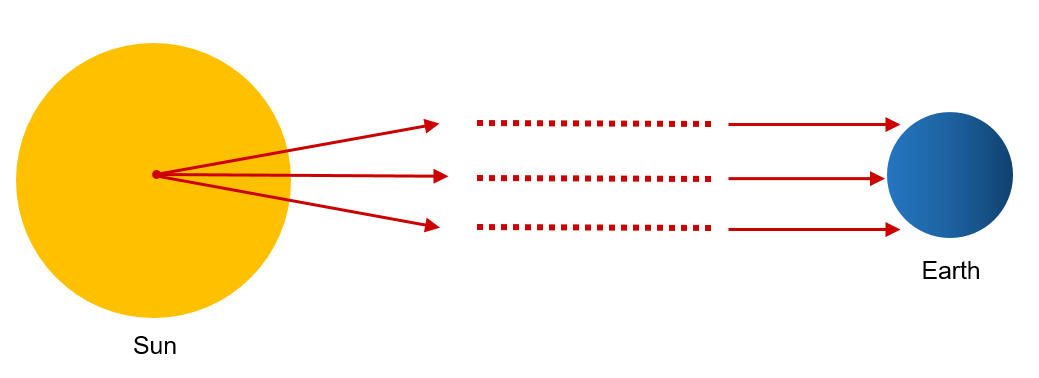
太阳光从太阳出发时是从中心往外辐射的,但由于日地距离远大于太阳和地球的尺度,到达地球的太阳光近乎是平行光。我们把这里的太阳光换成矢径 $\vec{r}$,便能理解这一近似。于是有 $$ \vec{r} \approx \vec{R} $$ $$ \Omega \approx \iint_S \frac{\vec{e_R} \cdot d\vec{S}}{R^2} = \frac{1}{R^2} \iint_S \vec{e_R} \cdot d\vec{S} = \frac{S_0}{R^2} $$
其中 $S_0$ 为物体表面在以 $\vec{\rm{e}_R}$ 为法向的平面上的投影面积。设物体 $A$ 和 物体 $B$ 的投影面积分别为 $S_A$ 和 $S_B$,最后可以得出它们互相张成的立体角 $$ \Omega_A = \frac{S_A}{R^2} $$ 同时易得等式 $$ S_A\Omega_B = S_B\Omega_A $$ $$ \Omega_B = \frac{S_B}{R^2} $$
这个等式可以应用于辐射测量或雷达探测中,这里就不再赘述了。