Python 的取模运算 r = m % n 相当于

# 或q = math.floor(m / n)
q = m // n
r = m - q * n

即取模的结果是被除数减去地板除的商和除数的乘积，这一规则对正数、负数乃至浮点数皆适用。

当 n 为正数时。显然任意实数 x 可以表示为 x = r + k * n，其中 0 <= r < n，k 是某个整数。那么有

x // n = floor(r/n + k) = k
x % n = x - x // n = r

即 x % n 的结果总是一个大小在 [0, n) 之间的实数 r。当 n = 10 时，以 x = 12 和 x = -12 为例：

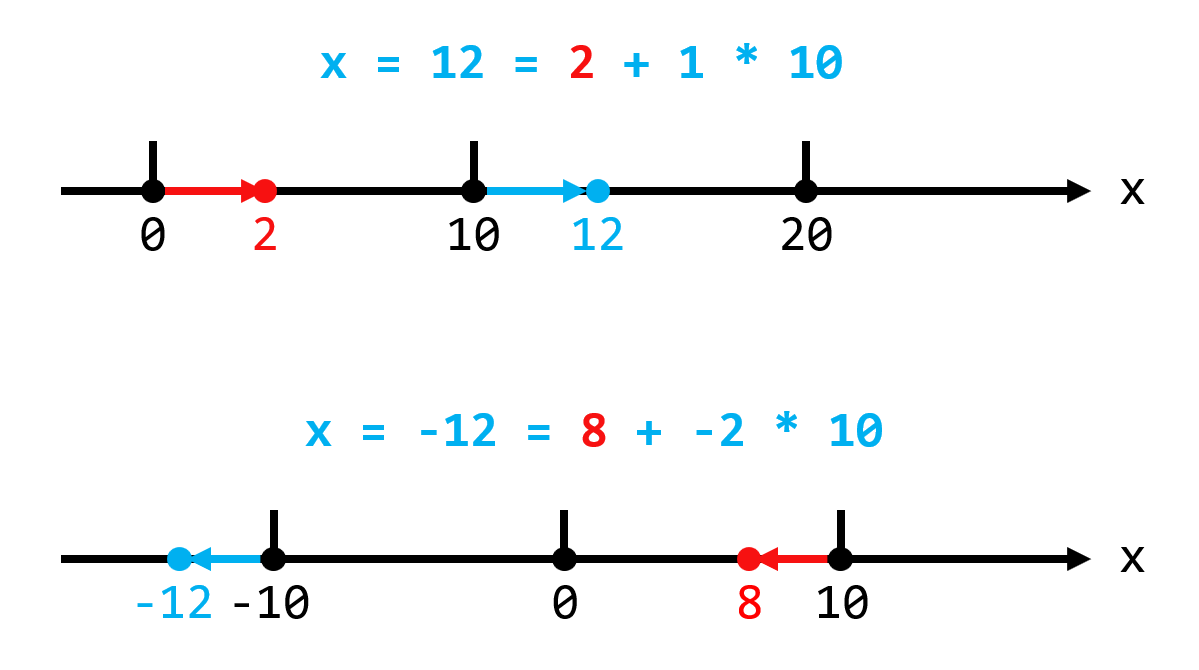
如果以 n 为一个周期，那么 x = 12 就相当于往右一个周期再走 2 格，x % n 会消去这个周期，剩下不满一个周期的 2；x = -12 相当于往左两个周期后再往右走 8 格，x % n 会消去这两个周期，剩下不满一个周期且为正数的 8。

再本质点说，取模运算就是在 [0, 10) 的窗口内进行“衔尾蛇”移动：

• 12 向右超出窗口两格， 12 % 10 = 2，即右边出两格那就左边进两格。
• -12 向左超出窗口 12 格，-12 % n = 8，即左边出 12 格那就右边进 12 格，发现还是超出左边两格，再从右边进两格，最后距离零点 8 格。

下面介绍取模运算的两个应用。

地球的经度以本初子午线为起点，自西向东绕行一圈，经度的数值从 0° 增长到 360°。不过经度还可以大于 360°，表示绕行一圈以上，甚至还可以是负数，表示自东向西绕行。显然这跟取模运算的衔尾蛇特性完美契合，通过取模运算可以将 [0, 360) 范围外的经度变换回这个范围内：

import numpy as np

lon = np.arange(-360, 720 + 1, 180)
print(lon)
print(lon % 360)

[-360, -180,    0,  180,  360,  540,  720]
[   0,  180,    0,  180,    0,  180,    0]

另外一个常用的经度范围是 [-180, 180)，即经度跨过太平洋上的对向子午线时经度会从正数跳变到负数。问题是如何将 [0, 360] 范围内的经度变换到 [-180, 180) 范围内。显然 [-180, 180) 是一个窗口，我们希望范围在 [180, 360] 的经度从窗口右边离开，再从窗口左边进入。但因为窗口范围不满足 [0, n) 的形式，所以不能直接取模，而是应该先向右偏移 180°，在正轴完成衔尾蛇移动后再偏移回负轴：

(lon + 180) % 360 - 180

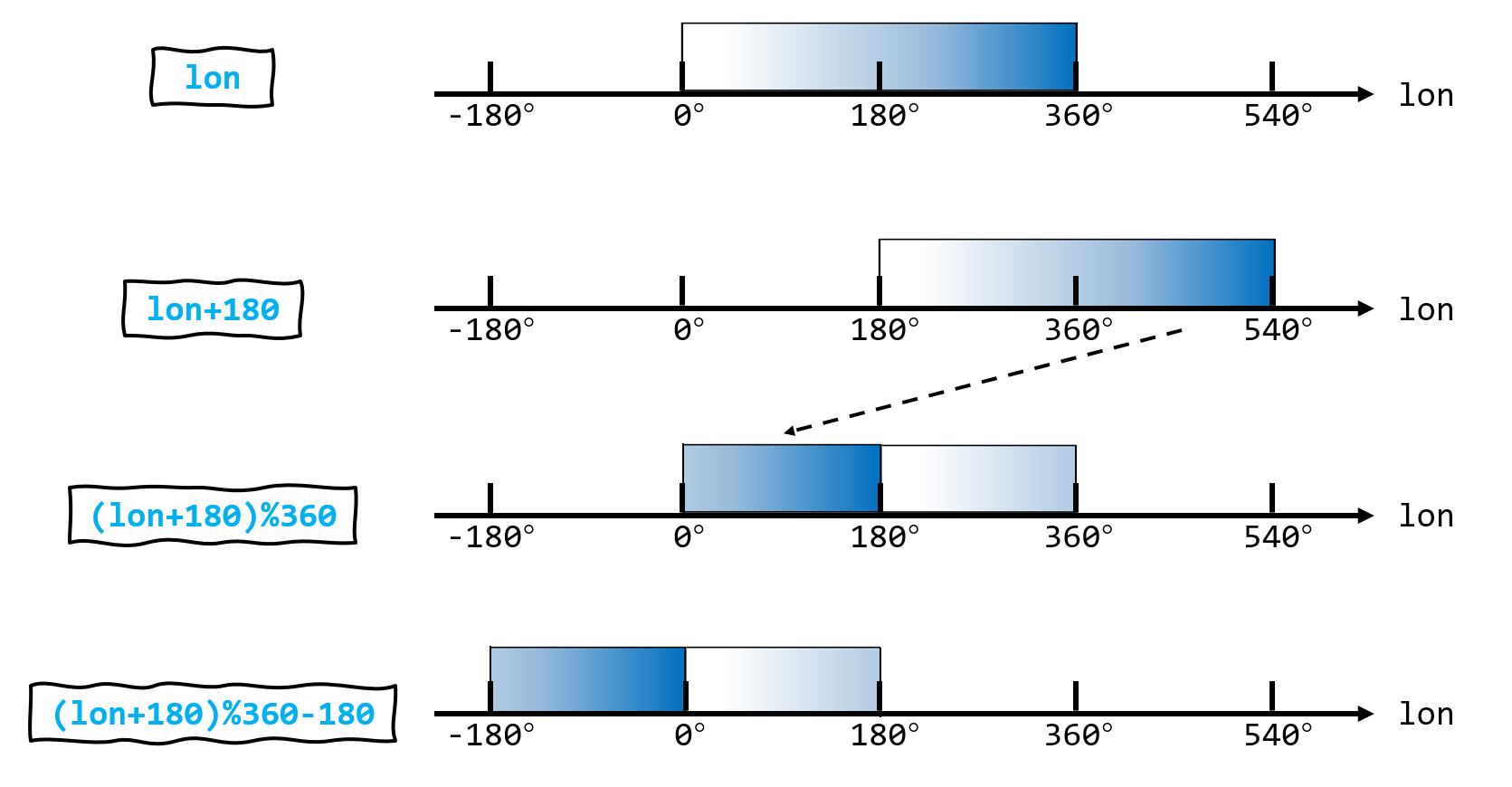
注意，这一算法中 180° 会被算到 -180°，360° 会被算到 0°：

lon = lon = np.arange(0, 360 + 1, 180)
print(lon)
print((lon + 180) % 360 - 180)

[    0,  180,  360]
[    0, -180,    0],

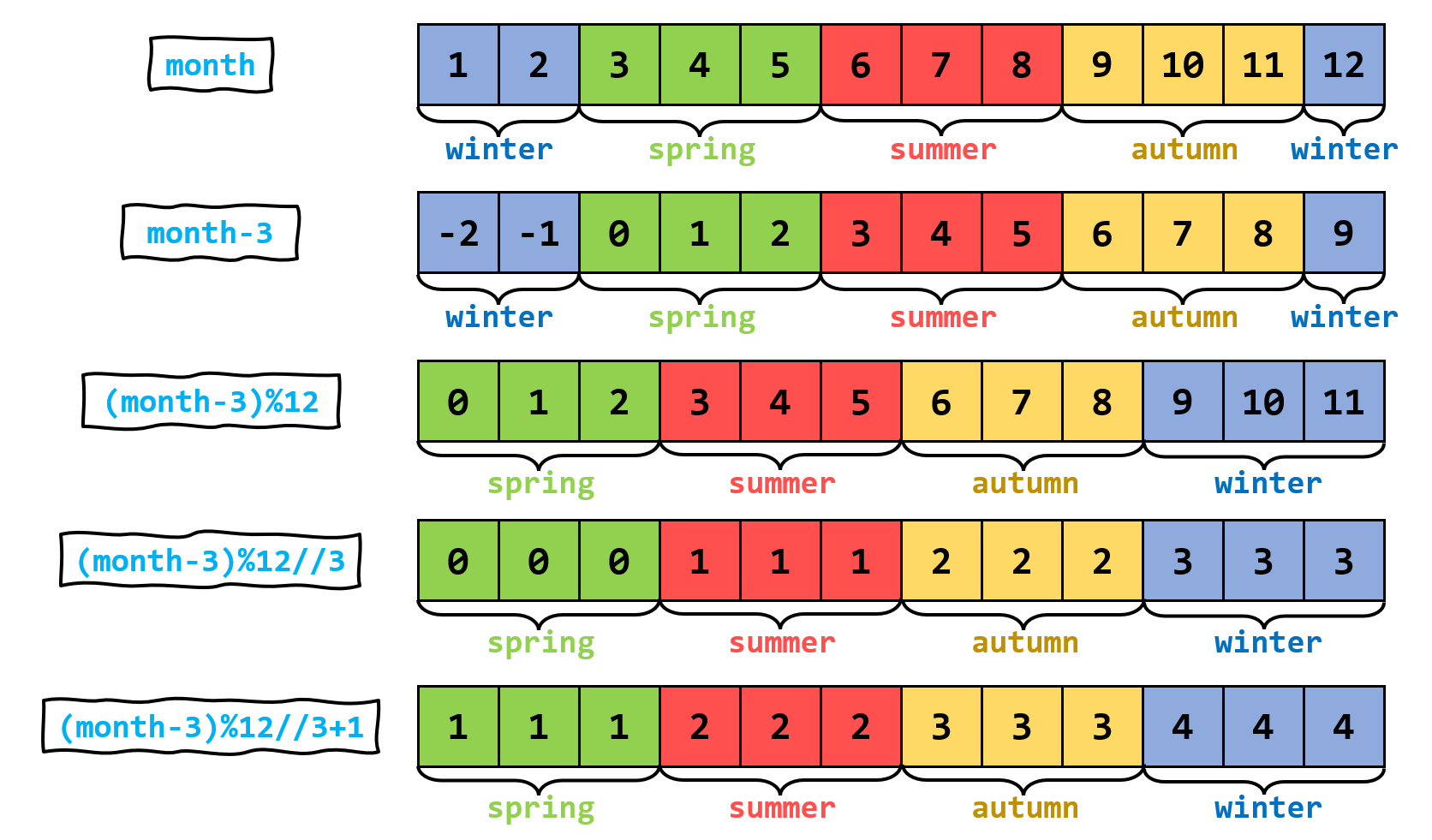
第二个应用是将月份换算成季节。气候学上春季指 3、4、5 月份，夏季指 6、7、8 月份，秋季指 9、10、11 月份，冬季指 12 月和来年 1、2 月。这里暂时不考虑冬季跨年的问题（可参考笔者的 Period 文章），只是将 [1, 12] 的月份映射到 [1, 4] 上，1、2、3、4 分别表示春夏秋冬。

首先可以想到，地板除能将 12 个月等分为 4 组：

month = np.arange(1, 13)
print(month)
print((month - 1) // 3 + 1)

[ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12]
[ 1,  1,  1,  2,  2,  2,  3,  3,  3,  4,  4,  4]

可惜春天是在 1、2、3 月的基础上向右偏移两个月；冬天是在 10、11、12 月的基础上向右偏移两个月，超出 12 月的部分从左边重新进入（即 1、2 月）。那么可以考虑通过取模把月份向左“旋转”两格，让春天排在前三格的位置，冬天排在最后三格的位置，这样就能应用地板除做分组了：

(month - 3) % 12 // 3 + 1

当然，这两个问题都可以用更简单的方式来解决：经度可以用 np.where(lon > 180, 360 - lon, lon) 转换，季节可以用 if 判断或字典来做映射。但取模运算能将你的代码精简至一行，同时方便迷惑其它读者（大雾）。