0. 前言

所谓 colormap（颜色表），就是将一系列颜色按给定的顺序排列在一起。其用处是，我们可以通过某种映射关系，将一系列数值映射到一张 colormap 上去，使不同大小的数值对应不同的颜色。这样一来，在绘制填色图时便能直观地用颜色来反映数值的分布。

在 Matplotlib 中，数值到颜色的映射关系可以用下面这张流程图来表示

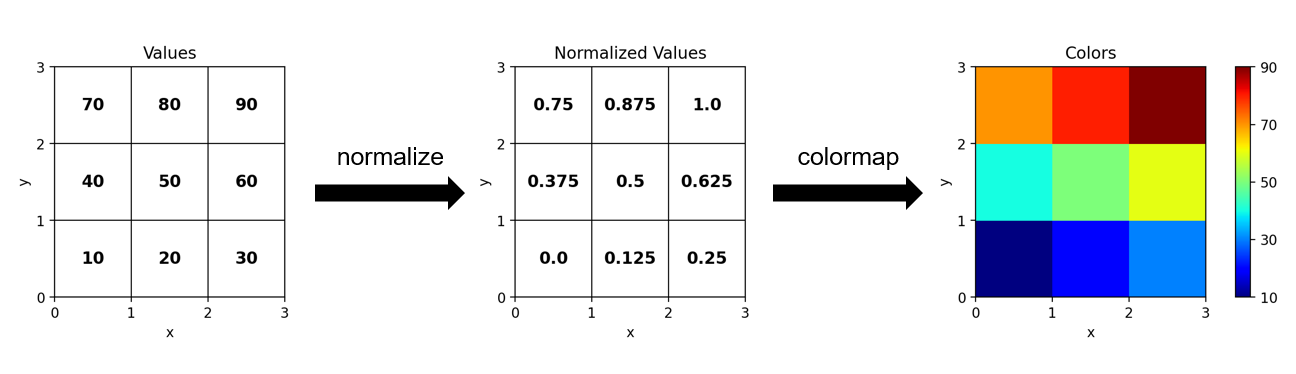
flowchart

图中分为前后两部分

  • 首先将数组归一化（normalize）到浮点型的 [0, 1] 范围（或整型的 [0, N - 1] 范围）上去。
  • 再把归一化的数组输入给 colormap，查询每个数值对应的颜色。

第二部分的映射关系是固定不变的，但第一部分的映射关系可以通过归一化相关的类加以改变，进而实现对数色标、对称色标、离散色标等一系列填色效果。

本文将会依次介绍 Colormap 类、Normalize 类，以及实际应用的例子。代码基于 Matplotlib 3.3.4。

（2022-01-17 更新：增加了一些解释说明，删掉了不实用的介绍，加入了 BoundaryNorm 实现的红蓝色标的例子。）

1. Colormap

很容易想到，一系列颜色可以用 (N, 3) 或 (N, 4) 形状的 RGB(A) 数组表示。但是 Matplotlib 中的 colormap 并非简单的数组，而是专门用一个 Colormap 类实现的，有着更加方便的重采样（resample）功能。内置的所有 colormap 存放在 matplotlib.cm 模块下，其外观可以在官网的 Choosing Colormaps in Matplotlib 页面看到。

Colormap 分为两个子类：ListedColormap 和 LinearSegmentedColormap，它们被存放在 matplotlib.colors 模块下。在介绍它们之前先做点准备工作

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as mcolors

def show_cmap(cmap, norm=None, extend=None):
    '''展示一个colormap.'''
    if norm is None:
        norm = mcolors.Normalize(vmin=0, vmax=cmap.N)
    im = cm.ScalarMappable(norm=norm, cmap=cmap)

    fig, ax = plt.subplots(figsize=(6, 1))
    fig.subplots_adjust(bottom=0.5)
    fig.colorbar(im, cax=ax, orientation='horizontal', extend=extend)
    plt.show()

1.1 ListedColormap

顾名思义，将所需的颜色全部列出来，便能生成这一类的 colormap。初始化参数为

ListedColormap(colors, name='from_list', N=None)

colors 是颜色名组成的列表或 RGB(A) 数组，name 和 N 分别是该 colormap 的名字和所含颜色数，不过自定义对象一般不需要取名，颜色数默认为 len(colors)，所以这两个参数基本用不上。这些参数随后会被赋给对象的同名属性。例如

colors = ['darkorange', 'gold', 'lawngreen', 'lightseagreen']
cmap = mcolors.ListedColormap(colors)
show_cmap(cmap)

listed_1 

In : cmap.colors
Out: ['darkorange', 'gold', 'lawngreen', 'lightseagreen']

In : cmap.N
Out: 4

文档中提到的 qualitative colormap 均为 ListedColormap，因为颜色有限且分隔明显，所以能定性反应数值的特征，如下图所示

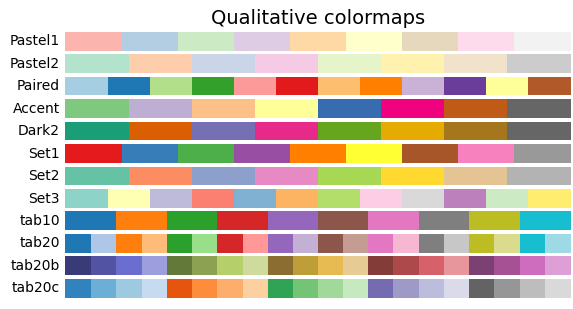
qualitative

以内置的 Set1 为例

In : cm.Set1.colors
Out:
((0.8941176470588236, 0.10196078431372549, 0.10980392156862745),
 (0.21568627450980393, 0.49411764705882355, 0.7215686274509804),
 (0.30196078431372547, 0.6862745098039216, 0.2901960784313726),
 (0.596078431372549, 0.3058823529411765, 0.6392156862745098),
 (1.0, 0.4980392156862745, 0.0),
 (1.0, 1.0, 0.2),
 (0.6509803921568628, 0.33725490196078434, 0.1568627450980392),
 (0.9686274509803922, 0.5058823529411764, 0.7490196078431373),
 (0.6, 0.6, 0.6))

In : cm.Set1.N
Out: 9

可以看到 colors 属性以嵌套元组的形式存储。

cmap 对象可以直接用数值参数调用，索引数值对应的 RGBA 值。根据数值是整型还是浮点型，对应关系也会有所不同，如下图所示

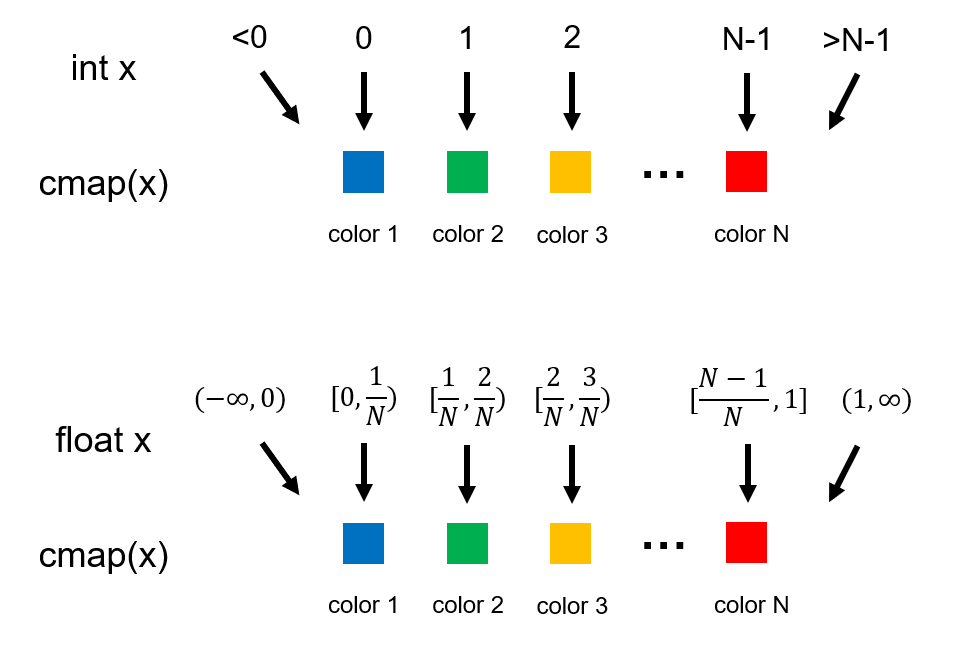
mapping_listed

当参数 x 为整数时，对应第 x - 1 个颜色；当 x 为浮点数时，根据它所在的区间决定颜色。当 x 超出 [0, N - 1] 或 [0, 1] 的范围时，对应于第一个和最后一个颜色。下面的例子里用两种方式获得了 cmap 中所有颜色的 RGBA 值

In : cmap(np.arange(cmap.N))
Out:
array([[1.        , 0.54901961, 0.        , 1.        ],
       [1.        , 0.84313725, 0.        , 1.        ],
       [0.48627451, 0.98823529, 0.        , 1.        ],
       [0.1254902 , 0.69803922, 0.66666667, 1.        ]])

In : cmap(np.linspace(0, 1, cmap.N))
Out:
array([[1.        , 0.54901961, 0.        , 1.        ],
       [1.        , 0.84313725, 0.        , 1.        ],
       [0.48627451, 0.98823529, 0.        , 1.        ],
       [0.1254902 , 0.69803922, 0.66666667, 1.        ]])

显然结果是相同的。再举个利用索引结果创建新 colormap 的例子

cmap_new = mcolors.ListedColormap(
    cmap(np.linspace(0, 1, 5))
)
show_cmap(cmap_new)

cmap_new 看起来会是这个样子

listed_2

因为给出的参数中，最后两个数落进了同一个区间，所以对应的颜色相同。

1.2 LinearSegmentedColormap

顾名思义，是通过线性分段构建的 colormap，需要给出红绿蓝三种成分的锚点，然后用线性插值的方式得出锚点间的颜色。直接初始化对象的方法较难理解，说实话我也没太看懂，所以这里介绍其辅助方法

LinearSegmentedColormap.from_list(name, colors, N=256, gamma=1.0)

name 是对象的名字，这回躲不掉必须填了；colors 是锚点的颜色，锚点对应的数值默认等距分布在 [0, 1] 区间上，不过可以在 colors 的每个颜色前指定数值；N 指定最后插值出几个颜色，默认为 256，所以基本看不出颜色间的间隔；gamma 是伽马校正的参数。例如

cmap1 = mcolors.LinearSegmentedColormap.from_list('cmap1', colors)
show_cmap(cmap1)

nodes = [0, 0.8, 0.9, 1]
cmap2 = mcolors.LinearSegmentedColormap.from_list(
    'cmap2', list(zip(nodes, colors))
)
show_cmap(cmap2)

linear_1

linear_2

第二个 colormap 因为黄色系的锚点到了 0.8 的位置，所以视觉上黄色占了很大面积。

大部分内置 colormap 都属于 LinearSegmentedColormap，例如文档中提到的 sequential colormap，因为颜色连续过渡自然，所以能定量反应数值的大小，如下图所示

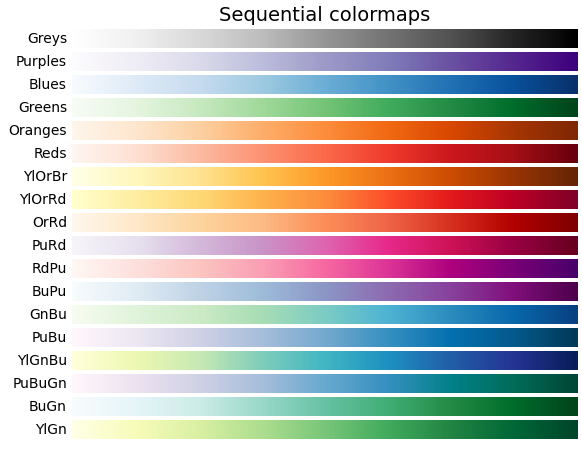
sequential

以内置的 jet 为例

In : cm.jet.colors
-------------------------------------------------------------------------
AttributeError: 'LinearSegmentedColormap' object has no attribute 'colors

In : cm.jet.N
Out: 256

即 LinearSegmentedColormap 虽然由 N 个颜色组成，但不能像 ListedColormap 那样把它们直接列举出来。cmap 同样可以被调用，当参数 x 为整数时，对应于第 x + 1 个颜色；当 x 为浮点数时，会通过线性插值获取相邻两个颜色中间的颜色。因此，LinearSegmentedColormap 的重采样不仅不会出现重复的颜色，还能得到更为连续渐变的颜色。不过有一说一，当颜色足够多时（即 N 很大时），两种 colormap 的区别就微乎其微了。

1.3 get_cmap 函数

有时我们希望通过重采样直接得到一个新的 colormap，而不是得到一组 RGBA 值，这个需求可以用 get_cmap 函数实现，例如对 jet 采样 8 个颜色

# 等价于cm.jet(np.linspace(0, 1, 8))
cmap = cm.get_cmap('jet', 8)

效果如下图，并且采样得到的 colormap 依旧为 LinearSegmentedColormap。

get_cmap

1.4 set_under、set_over 和 set_bad

1.1 节中提到过，直接调用 cmap 时，若参数 x 超出范围，那么会映射给第一个或最后一个颜色。而 cmap 的 set_under 方法能够改变 x < 0 时对应的颜色，set_over 方法能够改变 x > N - 1 或 x > 1 时对应的颜色。set_bad 则能改变缺测值对应的颜色（见 NumPy 系列：缺测值处理 最后一节）。

使用 fig.colorbar 方法画 colorbar 时，通过 extend 参数可以指定是否在 colorbar 两端显示出 under 与 over 的颜色。比如

cmap = cm.get_cmap('jet', 8)
cmap.set_under('black')
cmap.set_over('white')
show_cmap(cmap, extend='both')

set_cmap

1.5 修改内置 colormap

用 get_cmap 函数重采样得到的 colormap 可以直接用 set_xxx 系列方法进行修改，但对内置的 colormap 这样操作则会产生 MatplotlibDeprecationWarning。因为内置 colormap 都是全局对象，原地修改时会影响全局的效果。将来这一行为将会直接报错，官方建议先拷贝再修改。

import copy

cmap = copy.copy(cm.jet)
cmap.set_under('black')
cmap.set_over('white')

1.6 拼接内置 colormap

我们可以以内置的 colormap 为素材，自由拼接出新的 colormap。例如

colors_cool = cm.cool(np.linspace(0, 1, 128))
colors_spring = cm.spring(np.linspace(0, 1, 128))
colors_all = np.vstack((colors_cool, colors_spring))
cmap_merged = mcolors.ListedColormap(colors_all)
show_cmap(cmap_merged)

merged

2. Normalization

上一节的重点是，colormap 能把 [0, 1] 或 [0, N - 1] 范围内的值映射到颜色上，那么这一节就来叙述如何利用归一化的类把原始数据映射到 [0, 1] 或 [0, N - 1] 上。相关的类都存放在 matplotlib.colors 模块中，下面介绍最常用的几种。

2.1 Normalize

各种二维绘图函数在进行归一化时默认使用 Normalize 类，其它类也都继承自它。其参数为

Normalize(vmin=None, vmax=None, clip=False)

若给出了 vmin 和 vmax，调用创建的对象时会按线性关系 $$ y = \frac{x - vmin}{vmax - vmin} $$

将数据 x 映射为 y。显然只有 [vmin, vmax] 范围内的 x 会刚好映射到 [0, 1] 上，其它范围的 x 会映射出小于 0 或大于 1 的值。若不给定 vmin 和 max，默认用 x 的最小值最大值代替，此时 y 的范围一定是 [0, 1]。例如

x = np.arange(0, 6)
norm = mcolors.Normalize()

In : norm(x)
Out:
masked_array(data=[0. , 0.2, 0.4, 0.6, 0.8, 1. ],
             mask=False,
       fill_value=1e+20)

经 norm 归一化后的值可以传给 colormap，进而按第一节介绍的映射规则得到画图用的颜色。即便 y 超出了 [0, 1] 的范围，也可以映射给第一个或最后一个颜色（或者 set_under 和 set_over 指定的颜色）。换句话说，[vmin, vmax] 范围外的 x 自然对应于 colormap 两端的颜色。

clip 参数为 True 时，能把 [vmin, vmax] 范围外的 x 映射为 0 或 1，因此使 set_under 与 set_over 的设置失效。一般默认为 False 即可。

2.2 LogNorm

LogNorm 的参数与 Normalize 相同，会先对数据求对数后再进行线性映射 $$ y = \frac{\log_{10}(x) - \log_{10}(vmin)}{\log_{10}(vmax) - \log_{10}(vmin)} $$ 其中 vmin 和 vmax 必须为正数，否则会报错；x 可以小于等于 0，不过结果会缺测。例如

x = np.logspace(0, 3, 6)
norm = mcolors.LogNorm(vmin=1E0, vmax=1E3)

In : norm(x)
Out:
masked_array(data=[0.0, 0.2, 0.4, 0.6, 0.8, 1.0],
             mask=[False, False, False, False, False, False],
       fill_value=1e+20)

2.3 TwoSlopeNorm

将 [vmin, vmax] 分成两个区间，进行分段线性映射。参数为

TwoSlopeNorm(vcenter, vmin=None, vmax=None)

其中新增的 vcenter 是分段点，要求 vmin、vcenter 和 vmax 的值依次递增。映射的具体公式为 $$ y = \begin{cases} -\infty &\text{if} \quad x < vmin \newline \frac{(x - vmin)}{2(vcenter - vmin)} &\text{if} \quad vmin \le x < vcenter \newline \frac{(x - vcenter)}{2(vmax - vcenter)} + \frac{1}{2} &\text{if} \quad vcenter \le x \le vmax \newline +\infty &\text{if} \quad x > vmax \end{cases} $$ 其内部是用 np.interp 函数完成计算的，超出 [vmin, vmax] 范围的 x 设置为无穷大（np.inf）。

2.4 BoundaryNorm

除了线性和对数的映射，有时我们需要的映射关系像是往一组摆在一起的框里投球。例如下图这个例子

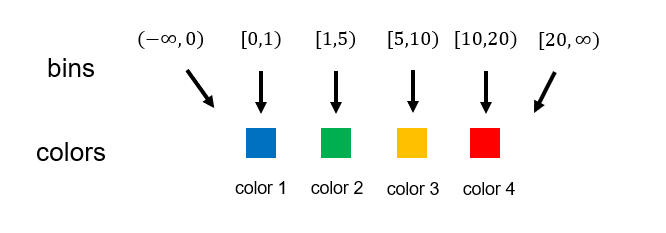
mapping_boundary

给出一系列边缘靠在一起的 bin（框子），原始数据落入第几个框（左闭右开区间），就对应于第几个颜色。因为这些框边缘的数值可以任意给定，所以很难用简单的函数表示。为了实现这种映射，这里引入 BoundaryNorm 类。其参数为

BoundaryNorm(boundaries, ncolors, clip=False, extend='neither')

boundaries 为给出的这些 bin 的边缘数值，要求单调递增；ncolors 指定对应的 colormap 含有的颜色数，要求数值大于等于 nbin = len(boundaries) - 1。当 ncolors = nbin 时，映射关系为 $$ y = \begin{cases} -1 &\text{if} \quad x < boundaries[0] \newline i &\text{if} \quad boundaries[i] \le x < boundaries[i+1] \newline nbin &\text{if} \quad x \ge boundaries[-1] \end{cases} $$ 可以看到，落入框中的 x 会被映射到 [0, nbin - 1] 区间，而没有落入框中的 x 会映射为 -1 或 nbin。当 ncolors > nbin 时，程序会通过线性插值（并取整）把上面的结果再映射到 [0, ncolors - 1] 区间。所以可以有两种使用方法：

  • ncolors 取 cmap.N，配合完整的 colormap。
  • ncolors 取 nbin，再把 colormap 采样到只含 nbin 个颜色。

个人一般会选用后者，这样能让每个 bin 与 colormap 中的颜色一一对应。

extend 参数会增大 nbin 以改变映射结果，直观效果是使第一个和最后一个 bin 对应的颜色区别于 under 和 over 时的颜色。考虑到会使映射关系变复杂，所以我一般不会去设置，但对该效果有需求的读者可以自己试试。下面是一个简单例子

bins = [0, 0.1, 0.5, 1.0, 5.0, 10.0]
nbin = len(bins) - 1
norm = mcolors.BoundaryNorm(bins, nbin)
x = [-1, 0.05, 0.2, 0.6, 2, 8, 12]

In : norm(x)
Out:
masked_array(data=[-1, 0, 1, 2, 3, 4, 5],
             mask=[False, False, False, False, False, False, False],
       fill_value=999999,
            dtype=int64)

2.5 其它归一化

除了上面介绍的四种，还存在关于中心对称线性映射的 CenteredNorm、关于零点对称对数映射的 SymLogNorm、任意幂律关系的 PowerNorm、自定义函数关系的 FuncNorm 等，这些都可以在 官方教程 里找到例子，此处就不详细介绍了。

3 实际应用

3.1 pcolor 和 contour 的异同

对于画马赛克图的 pcolor、pcolormesh 和 imshow 函数，我们在实际使用中并不需要手动进行数据的归一化和颜色索引，只需在调用函数时通过 cmap 和 norm 参数把 colormap 和归一化的类传入即可，绘图函数会自动计算数据和颜色的对应关系。cmap 默认为 viridis，norm 默认为无参数的 Normalize。下面是例子

# 生成测试数据.
x = np.linspace(0, 10, 100)
y = np.linspace(0, 10, 100)
X, Y = np.meshgrid(x, y)
Z = 1E3 * np.exp(-(np.abs(X - 5)**2 + np.abs(Y - 5)**2))

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# 直接给出vmin和vmax时会自动用它们创建Normalize.
im = axes[0].pcolormesh(
    X, Y, Z, shading='nearest',
    cmap=cm.jet, vmin=0, vmax=1000
)
cbar = fig.colorbar(im, ax=axes[0], extend='both')
axes[0].set_title('Normalize')

# 若在pcolormesh中给定了norm,就不能再指定vmin和vmax了.
im = axes[1].pcolormesh(
    X, Y, Z, shading='nearest',
    cmap=cm.jet, norm=mcolors.LogNorm(vmin=1E-3, vmax=1E3)
)
# 使用LogNorm时,colorbar会自动选用_ColorbarLogLocator来设定刻度.
cbar = fig.colorbar(im, ax=axes[1], extend='both')
axes[1].set_title('LogNorm')

plt.show()

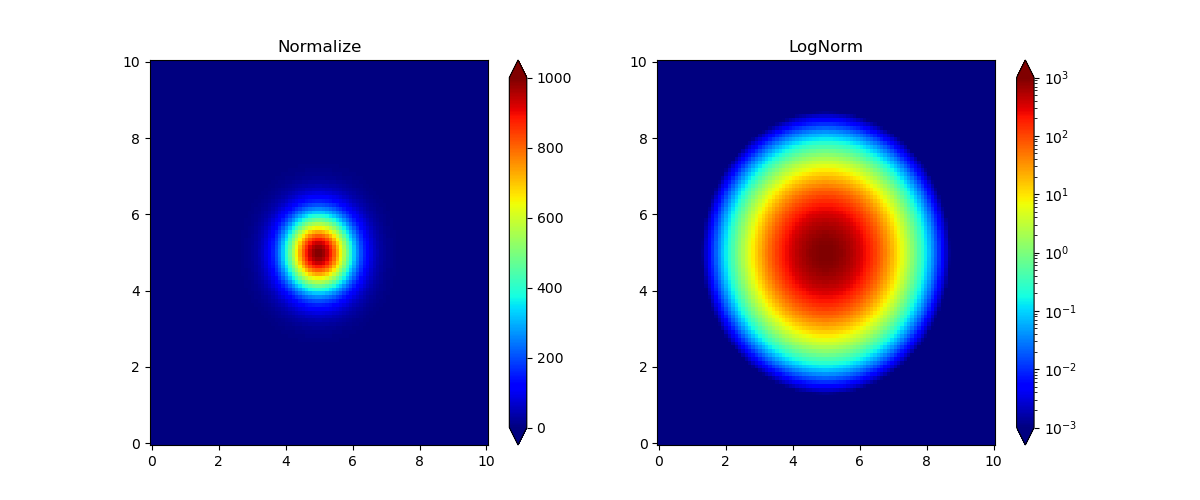
applications_1

可以看到 LogNorm 能让数据的颜色分布不那么集中。

而画等高线的 contour 和 contourf 则与 pcolor 有一些细节上的差异。这两个函数多了个 levels 参数，用于指定每条等高线对应的数值。norm 默认为 Normalize(vmin=np.min(levels), np.max(levels))，若给出了 vmin 和 vmax，则优先使用我们给出的值。对于 contour，每条等高线的颜色可以表示为 cmap(norm(levels))；对于 contourf，等高线间填充的颜色可以表示为

# 在norm不是LogNorm的情况下,layers计算为levels的中点.详请参考matplotlib.contour模块.
levels = np.asarray(levels)
layers = 0.5 * (levels[1:] + levels[:-1])
colors = cmap(norm(layers))

contourf 默认不会填充 levels 范围以外的颜色，如果有这方面的需求，可以用 extend 参数指定是否让超出范围的数据被填上 colormap 两端的颜色（或 set_under 和 set_over 指定的颜色）。并且当 contourf 指定了 extend 后，就不要在 colorbar 里指定了，否则会产生警告乃至错误。

举个同时画出等高线和填色图的例子，填色设为半透明

# 生成测试数据.
x = np.linspace(0, 10, 100)
y = np.linspace(0, 10, 100)
X, Y = np.meshgrid(x, y)
Z = (X - 5) ** 2 + (Y - 5) ** 2
# 将Z的值缩放到[0, 100]内.
Z = Z / Z.max() * 100

# 设置一个简单的colormap.
cmap = mcolors.ListedColormap(['blue', 'orange', 'red', 'purple'])
fig, ax = plt.subplots()
# contour和contourf默认使用levels的最小最大值作为vmin和vmax.
levels = np.linspace(10, 60, 6)
im1 = ax.contourf(X, Y, Z, levels=levels, cmap=cmap, alpha=0.5)
im2 = ax.contour(X, Y, Z, levels=levels, cmap=cmap, linewidths=2)
cbar = fig.colorbar(im1, ax=ax, ticks=levels)
# 为等高线添加标签.
ax.clabel(im2, colors='k')

plt.show()

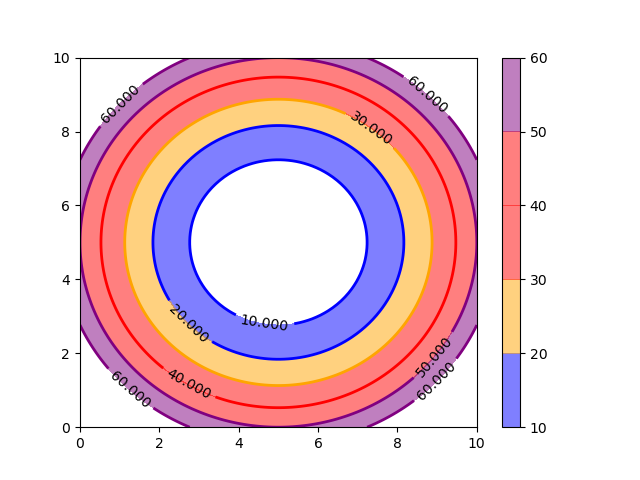
applications_2

可以看到，levels 范围以外的部分直接露出了白色背景。等高线的颜色与等高线之间的填色并不完全一致，这是 levels 和 layers 之间的差异导致的。以上提到的这些参数都可以在 contour 和 contourf 函数返回的 QuadContourSet 对象的属性中找到，有兴趣的读者可以自己调试看看。

3.2 BoundaryNorm 的应用

直接上例子

# 生成测试数据.
x = np.linspace(0, 10, 100)
y = np.linspace(0, 10, 100)
X, Y = np.meshgrid(x, y)
Z = X ** 2 + Y ** 2
# 将Z的值缩放到[0, 100]内.
Z = Z / Z.max() * 100

# 设置norm.
bins = [1, 5, 10, 20, 40, 80]
nbin = len(bins) - 1
norm = mcolors.BoundaryNorm(bins, nbin)
# 设置cmap.
cmap = cm.get_cmap('jet', nbin)
cmap.set_under('white')
cmap.set_over('purple')

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# 使用pcolormesh.
im = axes[0].pcolormesh(X, Y, Z, cmap=cmap, norm=norm, shading='nearest')
cbar = fig.colorbar(im, ax=axes[0], ticks=bins, extend='both')
axes[0].set_title('pcolormesh')


# 使用contourf.
im = axes[1].contourf(
    X, Y, Z, levels=bins, cmap=cmap, norm=norm, extend='both'
)
cbar = fig.colorbar(im, ax=axes[1], ticks=bins)
axes[1].set_title('contourf')

plt.show()

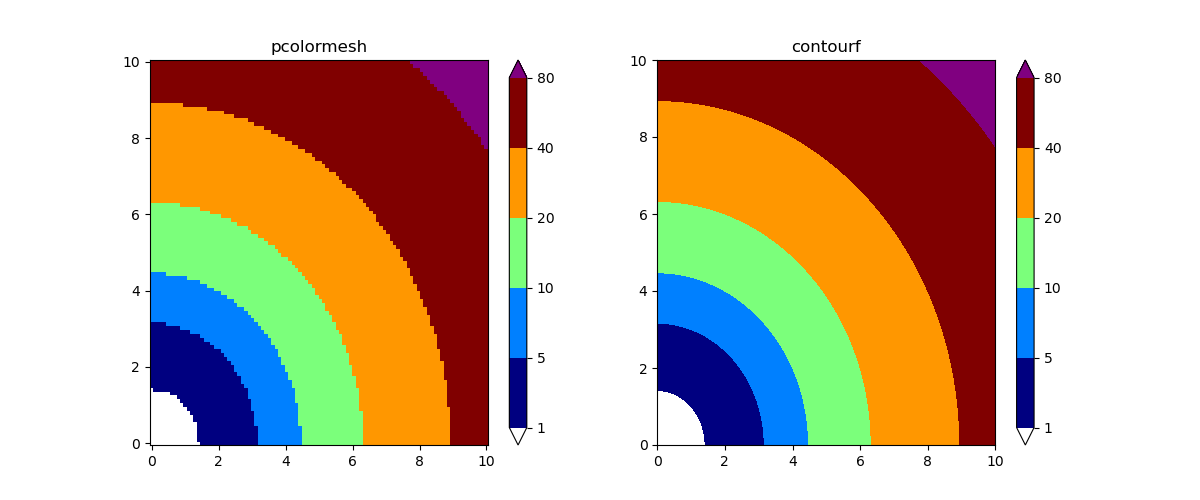
applications_3

在对 contourf 应用 BoundaryNorm 时，很容易联想到，等高线就相当于 bins 的边缘，等高线之间的填色正好对应于每个 bin 中的颜色，所以指定 levels=bins 是非常自然的。如果不这样做，contourf 默认会根据数据的范围，利用 MaxNLocator 自动生成 levels，此时由于 levels 与 bins 不匹配，填色就会乱套。

3.3 红蓝 colormap

当数据表示瞬时值与长时间平均值之间的差值时，我们常用两端分别为蓝色和红色的 colormap，并将数据的负值和正值分别映射到蓝色和红色上，这样画出来的图一眼就能看出哪里偏高哪里偏低。如果只需要以白色为中心，左右对称的 colormap，使用 Normalize 就行

Normalize(vmin=-10, vmax=10)

如果左右不对称，就改用 TwoSlopeNorm

TwoSlopeNorm(vmin=-5, vcenter=0, vmax=10)

既想要 BoundaryNorm 那种非线性的映射，又想让含有 0 的 bin 对应白色的话，可以基于 BoundaryNorm 自定义一个类

class CenteredBoundaryNorm(mcolors.BoundaryNorm):
    '''将vcenter所在的bin映射到cmap中间的BoundaryNorm.'''
    def __init__(self, boundaries, vcenter=0, clip=None):
        super().__init__(boundaries, len(boundaries) - 1, clip)
        boundaries = np.asarray(boundaries)
        self.N1 = np.count_nonzero(boundaries < vcenter)
        self.N2 = np.count_nonzero(boundaries > vcenter)
        if self.N1 < 1 or self.N2 < 1:
            raise ValueError('vcenter两侧至少各有一条边界')

    def __call__(self, value, clip=None):
        # 将BoundaryNorm的[0, N-1]又映射到[0.0, 1.0]内.
        result = super().__call__(value, clip)
        if self.N1 + self.N2 == self.N - 1:
            result = np.ma.where(
                result < self.N1,
                result / (2 * self.N1),
                (result - self.N1 + self.N2 + 1) / (2 * self.N2)
            )
        else:
            # 当result是MaskedArray时除以零不会报错.
            result = np.ma.where(
                result < self.N1,
                result / (2 * (self.N1 - 1)),
                (result - self.N1 + self.N2) / (2 * (self.N2 - 1))
            )

        return result

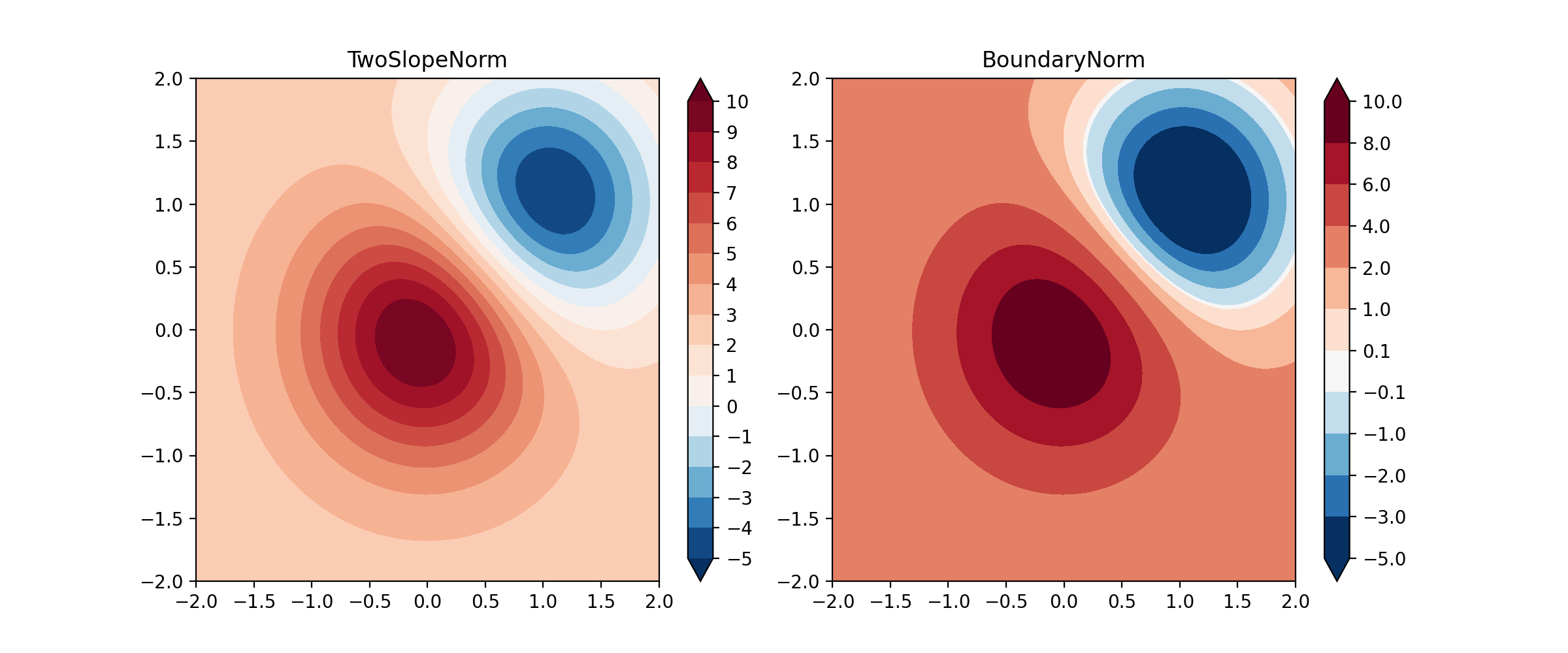
读者可以思考一下这个类的原理。下面展示 TwoSlopeNorm 和 CenteredBoundaryNorm 的效果

# 生成测试数据.
X, Y = np.meshgrid(np.linspace(-2, 2, 100), np.linspace(-2, 2, 100))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)
# 将Z的值缩放到[-5, 10]内.
Z = (Z - Z.min()) / (Z.max() - Z.min()) * 15 - 5

fig, axes = plt.subplots(1, 2, figsize=(12, 5))
fig.subplots_adjust(wspace=0.1)

# TwoSlopeNorm的图.
cf = axes[0].contourf(
    X, Y, Z,
    levels=np.linspace(-5, 10, 16),
    cmap='RdBu_r',
    norm=mcolors.TwoSlopeNorm(vmin=-5, vcenter=0, vmax=10),
    extend='both'
)
cbar = fig.colorbar(cf, ax=axes[0], ticks=cf.levels)
axes[0].set_title('TwoSlopeNorm')

# BoundaryNorm的图.
boundaries = [-5, -3, -2, -1, -0.1, 0.1, 1, 2, 4, 6, 8, 10]
im = axes[1].contourf(
    X, Y, Z,
    levels=boundaries,
    cmap='RdBu_r',
    norm=CenteredBoundaryNorm(boundaries),
    extend='both'
)
cbar = fig.colorbar(im, ax=axes[1], ticks=boundaries)
axes[1].set_title('BoundaryNorm')

plt.show()

applications_4

4. 结语

自 Matplotlib 3.5 起内置的 colormap 将被移入 matplotlib.colormap 模块，从中获取的 colormap 不再是全局对象，而是可以修改的拷贝；并且 get_cmap 函数以后可能被废弃。所以本文的代码不一定长期有效，望读者注意。

以上便是对 Matplotlib 中 colormap 的简要介绍，有错误的话烦请在评论区指出。而与 colormap 密切相关的 colorbar 的介绍请继续收看 Matplotlib 系列：colorbar 的设置。

参考链接

参考的全是 Matplotlib 官网的教程

Customized Colorbars Tutorial

Creating Colormaps in Matplotlib

Colormap Normalization

自定义 colormap 的介绍

Beautiful custom colormaps with Matplotlib