预测的 KPI：RMSE、MAE、MAPE 和 Bias

Nicolas Vandeput 发布在 Towards Data Science 上的文章，同时也是其著作《Data Science for Supply Chain Forecasting》中的一章。

为预测任务挑选一个合适的指标并没有想象中那么简单，所以这次我们来研究一下 RMSE、MAE、MAPE 和 Bias 的优缺点。剧透：MAPE 是其中最差的，别用。

fig1

衡量预测的准确度（或误差）并非易事，因为世上并不存在万能的指标。只有通过实验才能找出最适合你的关键性能指标（Key Performance Indicator, KPI）。后面我们将会看到，每个指标都各有优劣。

首先我们要区分预测的精度和偏差：

偏差（Bias） 表示历史平均误差。大概指你的预测平均下来偏高（即高估了需求量）还是偏低（即低估了需求量）。这个量能告诉你误差的总体方向。
精度（Precision） 衡量预测值到真实值的分散程度。这个量能告诉你误差的量级，但不反映误差的总体方向。

正如下图所示，我们希望预测能够既精确又没有偏差。

fig2

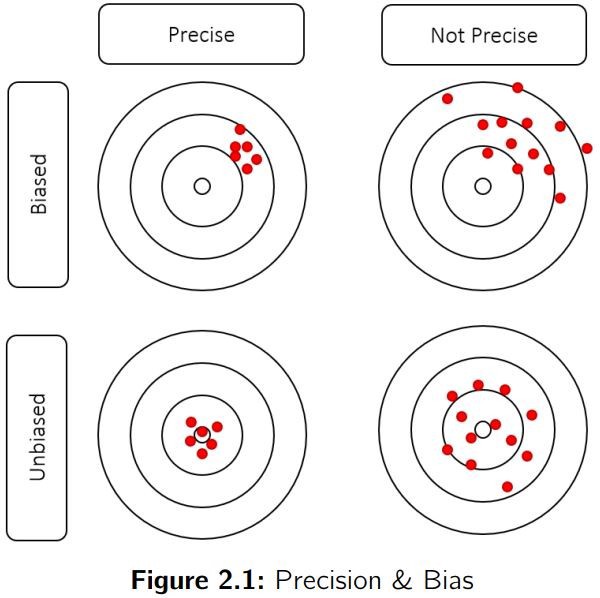
预测的 KPI

Error

误差（error）定义为预测量减去需求量。注意当预测高估需求时误差为正值，当预测低估需求时误差为负值。

$$ e_t = f_t - d_t $$

Bias

偏差（bias）定义为平均误差：

$$ bias = \frac{1}{n} \sum e_t $$

其中 $n$ 是既有需求值又有预测值的历史数据的数目。

因为正误差项会抵消负误差项，所以可以有偏差特别小，但精度却很低的预测模型。显然仅凭误差并不足以评估预测的精度，但如果预测偏差特别大，说明模型肯定哪儿有问题。

MAPE

平均绝对百分比误差（Mean Absolute Percentage Error, MAPE） 是衡量预测准确度最常用的 KPI 之一，每次预测的绝对误差除以对应的真实需求得到百分比误差，MAPE 即这些百分比误差的均值。

$$ MAPE = \frac{1}{n} \sum \frac{|e_t|}{d_t} $$

MAPE 真的是非常奇怪的一个预测 KPI。虽然企业管理者们都对它很熟悉，但它其实是个很糟糕的准确度指标。MAPE 的公式里每个误差都单独除以了需求，所以会是偏斜（skewed）的：在需求较低的时段高误差会强烈影响 MAPE。因此优化 MAPE 会导致预测倾向于低估需求。所以，咱还是避开它为妙。

MAE

平均绝对误差（Mean Absolute Error, MAE） 是一个很好的预测准确度 KPI。顾名思义，MAE 定义为绝对误差的平均值。

$$ MAE = \frac{1}{n} \sum |e_t| $$

该 KPI 的首要问题就是它的数值没有按平均需求的大小做调整。如果有人只告诉你某件商品的 MAE 是 10，你判断不了预测是好是坏。如果已知平均需求是 1000，那么预测效果非常好；但如果平均需求是 1，那么预测准确度就非常差。为了解决这个问题，通常将 MAE 除以平均需求换算成百分数：

$$ MAE% = \frac{\frac{1}{n} \sum |e_t|}{\frac{1}{n} \sum d_t} = \frac{\sum |e_t|}{\sum d_t} $$

混淆 MAPE/MAE：似乎不少从业者也管上面的 MAE 公式叫 MAPE，这会导致很多误解。所以我建议你在和别人讨论预测误差时直接展示误差是怎么计算的，以防鸡同鸭讲。

RMSE

均方根误差（Root Mean Square Error, RMSE） 是一个稍微有点奇怪，但也很好用的 KPI，这一点我们后面再详细讨论。定义是对误差的平方求平均值后再求平方根。

$$ RMSE = \sqrt{\frac{1}{n} \sum e_t^2} $$

类似 MAE，RMSE 同样没有按需求的大小做调整，因此这里定义 RMSE%：

$$ RMSE% = \frac{\sqrt{\frac{1}{n} \sum e_t^2}}{\frac{\sum d_t}{n}} $$

实际上很多算法（尤其是机器学习领域）都基于与之相关的均方误差（Mean Square Error, MSE）。

$$ MSE = \frac{1}{n} \sum e_t^2 $$

很多算法采用 MSE 是因为算起来比 RMSE 更快，操作起来更简单。但它的问题是误差平方后量纲与原始误差不同，导致我们无法将其与原始需求的大小联系起来。因此，我们在评估统计预测模型时不会用到 MSE。

误差权重的问题

相比 MAE，RMSE 并没有平等对待所有误差，而是会给大误差以更高的权重。这意味着一个特别大的误差就足以使 RMSE 变得很差。下面以一条虚构的需求时间序列为例。

fig3

假设我们想比较两组只有最后一个时段的预测值不同的预测：相比真实值，预测 #1 低估了 7 个单位，而预测 #2 仅低估了 6 个单位。

fig4

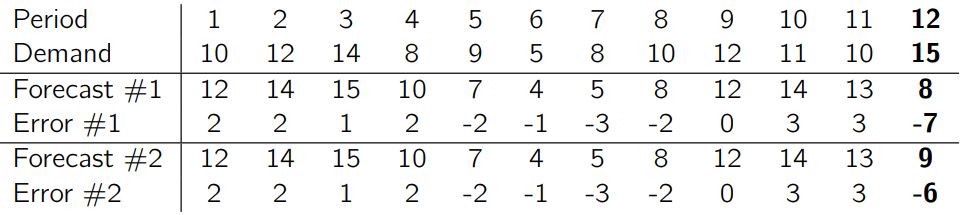
这两组预测的 KPI 如下所示：

fig5

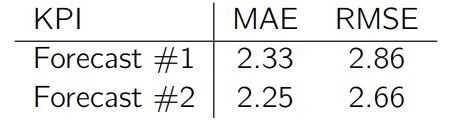
有趣的是，减小最后一个时段一个单位的误差，使得总的 RMSE 降低了 6.9%（从 2.86 变为 2.66），而 MAE 仅降低了 3.6%（从 2.33 变为 2.25），即 MAE 受到的影响几乎只有 RMSE 的一半。显然，RMSE 强调那些最显著的误差，而 MAE 给予每个误差相同的重要性。你可以试试在预测最准确的那几个时段里减小误差，看看会对 MAE 和 RMSE 产生什么影响。

剧透：RMSE 几乎不受影响。

之后我们会看到，RMSE 还有些别的有趣的性质。

你想预测什么？

前面过了一遍这些 KPI（bias, MAPE, MAE, RMSE）的定义，但仍不清楚选择不同的 KPI 对我们的模型来说有多大差别。有人可能觉得用 RMSE 替代 MAE，或用 MAE 替代 MAPE 是无关紧要的，但事实并非如此。

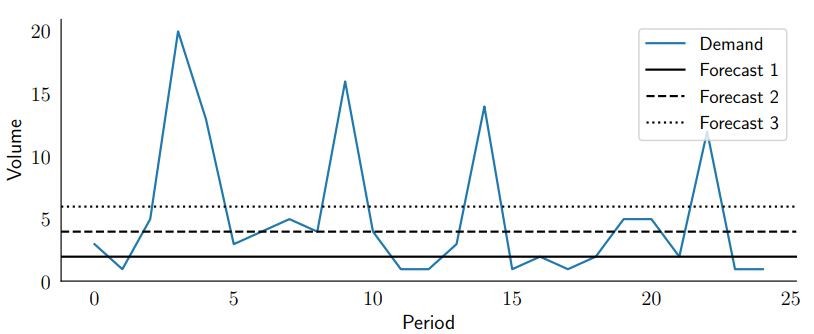
让我们用一个简单的例子来说明这一点。考虑一个每周需求量又低又平，但不时有大单子的产品（可能是促销或客户批量采购）。下面是目前为止观测到的每周需求量：

fig6

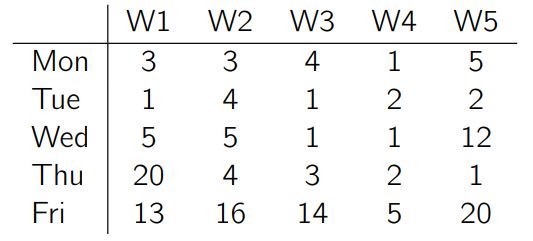
接着假设我们对这一产品做了三种预测：第一种预测每天 2 件，第二种 4 件，第三种 6 件。下面画出观测到的需求量和我们做的预测：

fig7

以 bias、MAPE、MAE 和 RMSE 为指标看看这些预测在这段时期的效果：

fig8

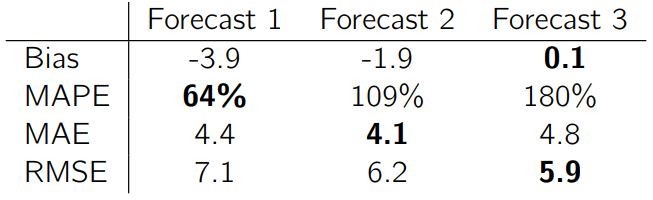
只看 MAPE 的话第一种预测最好，只看 MAE 的话第二种预测最好。第三种预测在 RMSE 和 bias 上都是最优的（但在 MAE 和 MAPE 上是最差的）。现在揭晓这些预测是怎么做出来的：

预测 1 就是随便选了个很低的值。
预测 2 取的是需求的中值 4。
预测 3 是平均需求。

中值 vs. 平均值——数学优化

在进一步讨论其它预测 KPI 之前，让我们花些时间理解一下为什么用中值作为预测会导向不错的 MAE，而用平均值会导向不错的 RMSE。

下面会有一点点数学，如果你对这些方程不熟悉的话也不必气馁，直接跳到关于 RMSE 和 MAE 结论的部分就行。

RMSE

首先从 RMSE 开始：

$$ RMSE = \sqrt{\frac{1}{n} \sum e^2_t} $$

为了简化后续的代数运算，这里采用简化版的均方误差（MSE）：

$$ MSE = \frac{1}{n} \sum e^2_t $$

如果你将 MSE 设为预测模型的优化目标，就需要最小化 MSE，即令其导数为零：

$$ \frac{\partial{MSE}}{\partial{f_t}} = \frac{\frac{1}{n} \sum (f_t - d_t)^2}{\partial{f_t}} $$

$$ \frac{2}{n} \sum (f_t - d_t)= 0 $$

$$ \sum f_t = \sum d_t $$

译注：这里设每一时刻的预测都相同，即 $f_t$ 是定值。

结论：为了优化预测的 MSE，模型需要以预测之和等于需求之和为目标，即优化 MSE 会产生平均水平上正确的预测，因此预测也是无偏差的。

MAE

接着对 MAE 做同样的处理：

$$ \frac{\partial{MAE}}{\partial{f_t}} = \frac{\partial{\frac{1}{n} \sum |f_t - d_t|}}{\partial{f_t}} $$

因为

$$ |f_t - d_t| = \begin{cases} f_t - d_t, & d_t < f_t \newline d_t - f_t, & d_t \ge f_t \end{cases} $$

且

$$ \frac{\partial{|f_t - d_t|}}{\partial{f_t}} = \begin{cases} 1, & d_t < f_t \newline \text{未定义}, & d_t = f_t \newline -1, & d_t > f_t \end{cases} $$

所以

$$ \frac{\partial{MAE}}{\partial{f_t}} = \frac{1}{n} \sum \begin{cases} 1, & d_t < f_t \newline -1, & d_t > f_t \end{cases} $$

结论：要优化 MAE（使其导数为零），比预测值高的需求应该和比预测值低的需求一样多，换句话说就是我们要找一个能将数据集等分成两份的值，而这恰好就是中值的定义。

MAPE

不幸的是 MAPE 的导数就没有如此优雅和直接的性质了。简单来说，MAPE 会将预测推向非常低的值，因为它给需求较低时的预测误差分配了更高的权重。

结论

如上所示，对 RMSE 的优化会导向平均水平上的正确预测。与之相反的是，对 MAE 的优化试图一半时间高估需求，一半时间低估需求，这意味着以中值为优化目标。我们必须理解 MAE 和 RMSE 在数学源头上的巨大差异：前者的目标是中值，后者的目标是平均值。

MAE 还是 RMSE——选哪个更好？

以需求的中值为目标更坏，还是以平均值为目标更坏？其实答案并不是非黑即白的，后面的讨论里将会看到，每种方法都各有优劣，只有通过实验才能找出对当前数据集最合适的方法。你甚至可以同时使用 RMSE 和 MAE。

让我们花时间讨论一下选 RMSE 或 MAE 会对 bias、离群值敏感度和间歇性需求的影响。

Bias

你会发现许多产品需求的中值和平均值都不相等，需求很可能是这儿那儿有几个峰，导致其概率分布是偏斜的。这种偏斜的需求分布在供应链中普遍存在，因为高峰可能是定期促销或客户大批采购造成的。这也导致需求的中值要比平均值小，如下图所示：

fig9

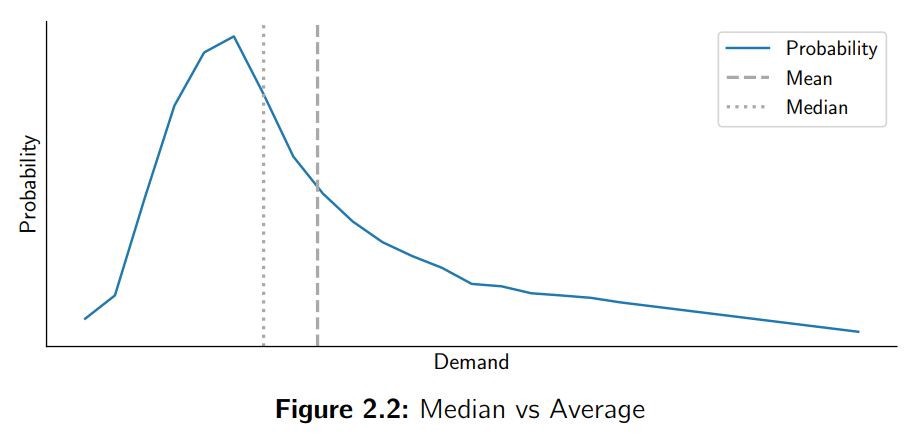
译注：图中的右偏分布一般满足众数 < 中值 < 平均值，但也存在反例。

这意味着优化 MAE 的预测会产生 bias，而优化 RMSE 的预测则是无偏的（因为目标就是平均值）。毫无疑问，这是 MAE 的主要缺点。

离群值的敏感度

正如我们在前面讨论的，RMSE 会给最高的误差以更高的权重。这一性质的代价是：对离群值很敏感。让我们想象一个有着如下规律的商品。

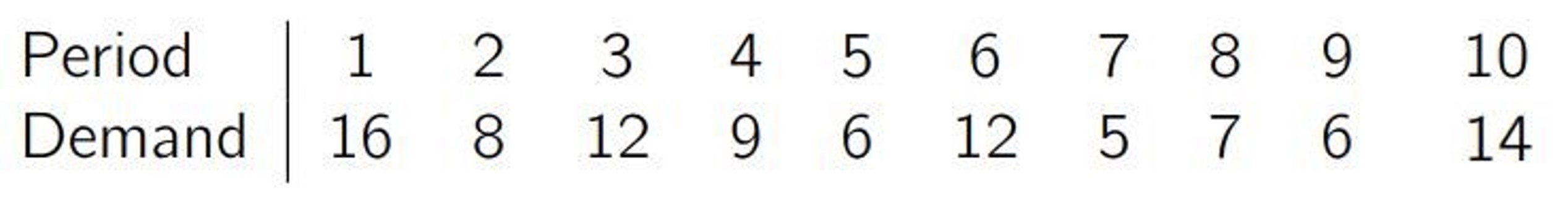
fig10

序列的中值是 8.5，平均值是 9.5。我们已经观察到，优化 MAE 会预测出中值（8.5），并且平均来看低估了 1 个单位（bias=-1）。你可能倾向于最小化 RMSE，预测出平均值（9.5）以避免有偏差的情况。然而，假设我们将最后一个需求值改为 100：

fig11

中值仍为 8.5（没有变！），但平均值现在变成了 18.1。这种情况下你就很可能改用中值做预测。

一般来说，中值在面对离群值时要比平均值更健壮（robust），这点在供应链环境中尤为关键，因为受编码错误或需求高峰（市场营销、促销、现货交易）等因素影响，我们会碰到很多离群值。

那对离群值的健壮性一定是个好性质吗？答案是不。

间歇性需求

不幸的是，对离群值的健壮性可能会给有间歇性需求的商品带来非常恼人的影响。

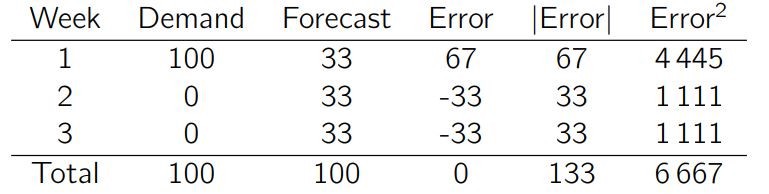
假设我们向客户销售一样产品，其利润非常高，但我们唯一的客户只在三周里的某一周下订单，且时间上看不出任何规律。这位客户每次总是订购 100 件，因此我们每周需求量的平均值是 33 件，中值是……0。

我们必须为该产品做每周的预测，假设我们的第一种预测方案是取平均需求（33 件），那么长期来看，总的平方误差是 6667（RMSE 是 47），总的绝对误差是 133（MAE 是 44）。

fig12

改用中值（0）做预测的话，总的绝对误差是 100（MAE 是 33），总的平方误差是 10000（RMSE 是 58）。

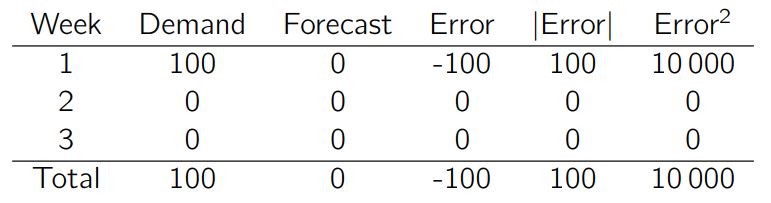
fig13

正如我们所看到的，对间歇性需求来说 MAE 是个很糟糕的 KPI。一旦你有超过一半的时刻没有需求，那么最优的预测是……0！

结论

MAE 能防御异常值，而 RMSE 能确保我们的预测无偏差。那你应该用哪个指标呢？可惜并不存在明确的答案。作为一名供应链数据科学家，你应该动手做实验：如果使用 MAE 作为 KPI 会导致高 bias，你可能要换用 RMSE；如果数据集里有很多离群值，导致预测偏斜，那你可能要换用 MAE。

值得注意的是，你可以选择一个或多个 KPI（通常是 MAE 和 bias）来汇报预测误差，但使用另一个 KPI（也许是 RMSE？）取优化模型。

最后提一个关于低需求量商品的技巧：将需求聚合到更长的时间范围上。例如，如果每周的需求很低，你可以尝试做月度乃至季度的预测，之后再通过简单的除法将预测拆分到原先的时间范围上。这个技巧允许你用 MAE 作为 KPI，同时能平滑需求峰值。