最近又碰到了给出地球上两点的经纬度,然后计算它们之间距离的问题。之前曾经通过查维基写过简单的博文,不过现在实践时发现博文里问题较多,故重撰如下。
地球的形状
为了计算地球上两点之间的距离,首先需要对地球的形状有个概念,以定义距离的几何表示。我们的一般常识是:地球是一个赤道方向略长、两极方向略短的椭球,且表面有着不规则起伏的地形。这种形状肯定无法直接计算,所以希望能简化为一个能用简单数学式子描述的形状。下面是一个简单且夸张的图示
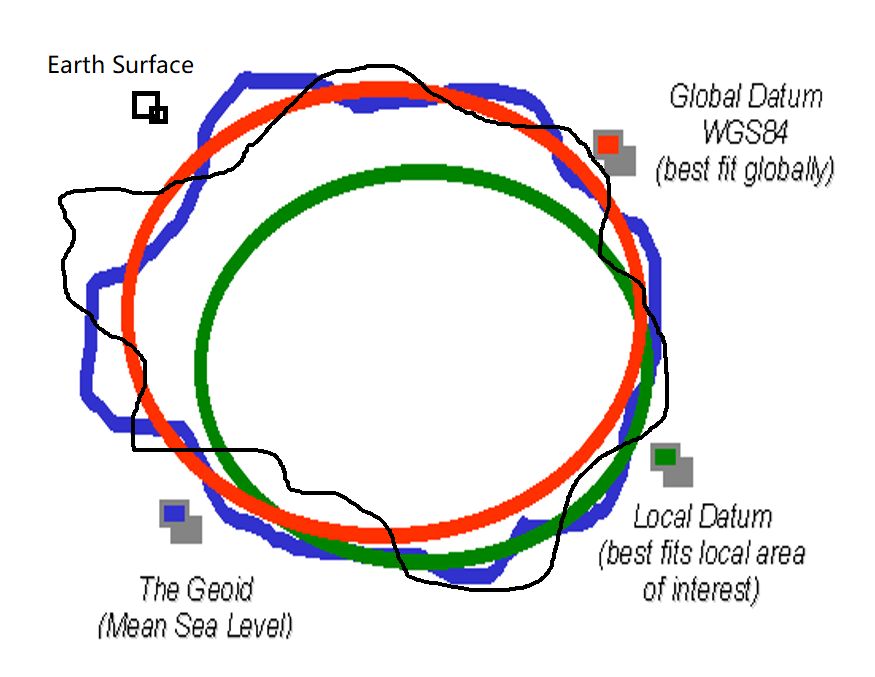
黑线表示地球的固体表面,因为地形起伏而显得不规则。不过这里只是夸张的画法,地形落差相对于地球半径而言其实微乎其微。黑线以上的蓝线是海平面,假设作为重力位能等势面的海平面能延伸到大陆内部,那么真实的海平面可以和假想的海平面共同构成一个封闭曲面,称为大地水准面(geoid)。由于地球内部质量分布不均,不同方向上重力有差异,所以大地水准面也会有些不规则。为了进一步简化,考虑用一个旋转椭球体去拟合大地水准面,拟合结果即为地球椭球体(earth ellipsoid)。因为地球椭球体可以用简单的数学式子描述,所以非常便于计算经纬度和海拔。对拟合效果的不同定义能导致不同的地球椭球体,例如考虑全球的拟合效果,常用 WGS84 坐标系(图中红线);而考虑区域的拟合效果时,会设计局地的坐标系(图中绿线)。
如果还想偷懒,可以进一步把旋转椭球体简化为球体。例如,在 WGS84 坐标系中,赤道方向半径 $a = 6378.1370\ \rm{km}$,两极方向半径 $b = 6356.7523\ \rm{km}$,椭球扁率 $f$ 为 $$ f = \frac{a-b}{a} \approx 0.003 $$ 因为扁率足够低,所以可以进一步近似为球体。图示如下
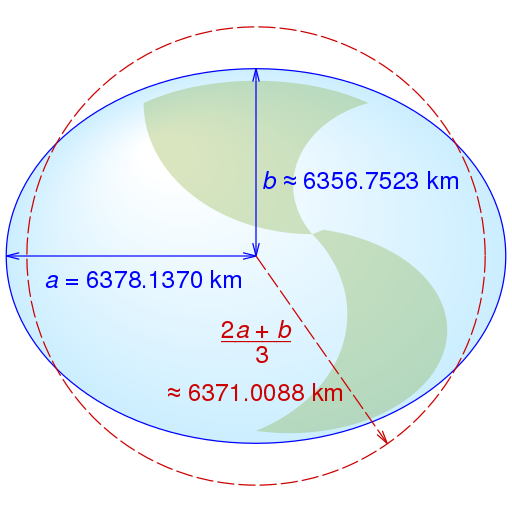
WGS 标准定义地球的平均半径 $R$ 为 $$ R = \frac{2a+b}{3} \approx 6371\ \rm{km} $$ Wiki 上说当球体取这一半径时能减小球体与椭球体在估计两点间距离时的误差,具体来源有待查证。总之,利用上述简化的形状模型,便能着手计算地球上两点间的距离。下面先从最简单的球体开始介绍。
球体上两点间的距离
假设地球是一个 $R = 6371\ \rm{km}$ 的球体,如下图所示
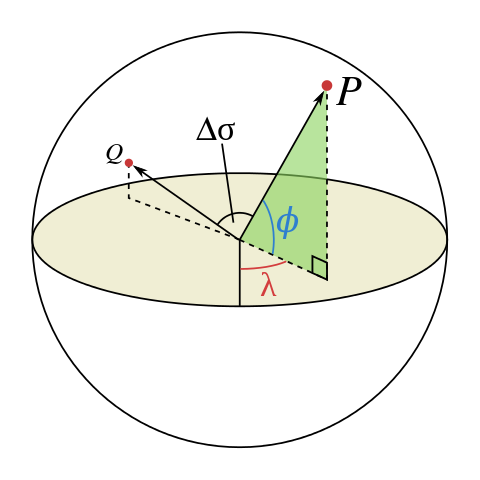
球坐标系中以北极方向为 $z$ 轴,赤道平面为 $xy$ 平面,球面上一点 $P$ 的经度和纬度分别为 $\lambda$ 和 $\phi$,取值范围为 $$ \lambda \in [-180^\circ, 180^\circ] \quad \text{or} \quad [0^\circ, 360^\circ] $$
$$ \phi \in [-90^\circ,90^\circ] $$
球面上两点间的距离指的是两点间长度最短的弧线,由于这一弧线肯定位于两点所在的大圆上,所以又称作大圆距离(great-circle distance)。首先来讨论一下经线和纬线上两点间的距离。
同一经线上的两点经度相同,纬度相差 $\Delta \phi$。由于经线都是半个大圆弧,所以两点间的距离直接由弧长公式得到 $$ \Delta d = R \Delta \phi $$ 容易看出,经线上纬度每相差 1°,距离相差约 111 km。
同一纬线上的两点纬度相同,经度相差 $\Delta \lambda$。与经线不同,纬线(或者说纬圈)是球面上的小圆,计算距离差时,首先把球的半径 $R$ 乘上 $\cos \phi$ 转化为小圆半径,再套用弧长公式 $$ \Delta d = R \cos \phi \Delta \lambda $$ 容易看出,赤道纬线上经度相差 1° 时,距离差依旧是 111 km 但纬度越高,这一距离越小。例如对于纬度 40°N 的北京,纬线上 1° 仅相当于 85 km。越靠近两个极点,距离就越接近 0。经线和纬线上的距离公式可以用下面这张图来总结
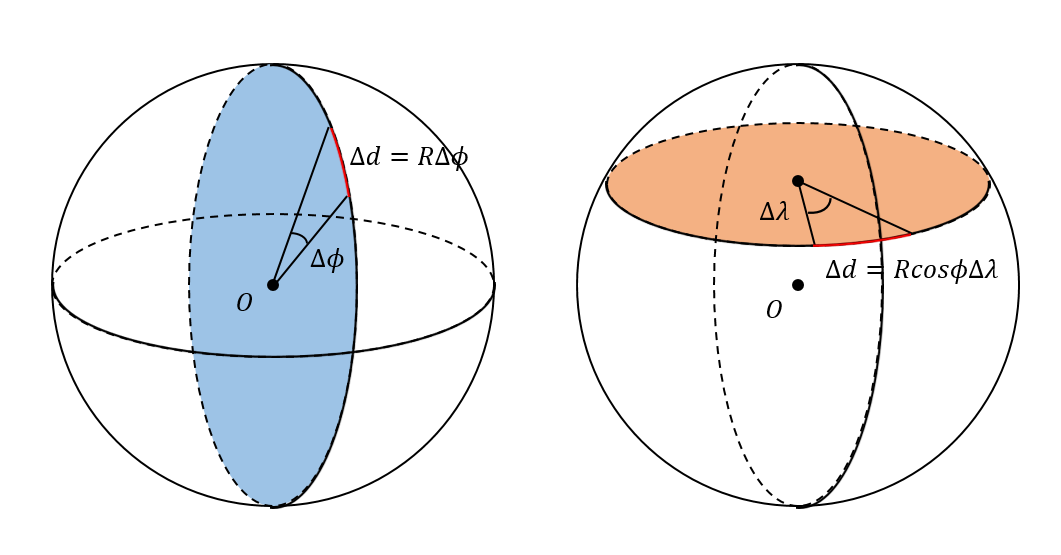
需要注意,公式中的 $\Delta \phi$ 和 $\Delta \lambda$ 在计算时需要转换为弧度单位。通常而言,在中低纬度地区为了方便,可以说 $1^\circ \approx 111\ \rm{km}$。
说完经线和纬线上的距离,接着拓展为球体上任意两点间的距离。设球面上有两个点 $P(\lambda_1, \phi_1)$ 和 $Q(\lambda_2, \phi_2)$,这两点间的距离即过 $P$ 点和 $Q$ 点的大圆上的弧 $PQ$ 的长度 $\Delta d$,如下图所示
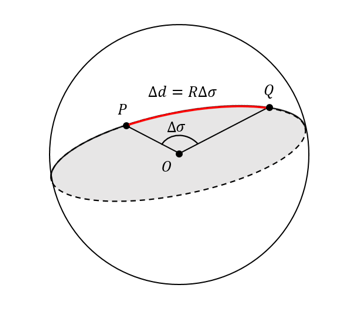
显然弧长 $\Delta d$ 与弧 $PQ$ 的圆心角 $\Delta \sigma$ 满足 $$ \Delta d = R \Delta \sigma $$ 所以计算距离的问题转化为如何计算圆心角 $\Delta \sigma$。由球面三角学中的球面余弦定理 $$ \Delta \sigma = \arccos (\sin \phi_1 \sin \phi_2 + \cos \phi_1 \cos \phi_2 \cos (\Delta \lambda)) $$ 其中 $\Delta \lambda$ 的正负不影响结果(后面将会出现的 $\Delta \phi$ 也是),最后得到的 $\Delta \sigma$ 的范围是 $[0,\pi]$。然而当两个点特别靠近时,$\arccos$ 括号内的值接近于 1,而 $\arccos$ 函数在这一点附近的变化率较大,计算时的舍入误差会因此变大。所以另外会使用数值上更加稳定的 haversine 公式。首先定义半正矢函数 $$ \rm{hav}\ \theta = \sin^2 \frac{\theta}{2} $$ 带入到球面余弦定理的公式中,易得 $$ \begin{align} \Delta \sigma &= \rm{archav}(\rm{hav}(\Delta \phi) + \cos \phi_1 \cos \phi_2 \rm{hav}(\Delta \lambda)) \newline &= 2 \arcsin \sqrt{\sin^2(\frac{\Delta \phi}{2}) + \cos \phi_1 \cos \phi_2 \sin^2(\frac{\Delta \lambda}{2})} \end{align} $$ 当两个点特别靠近时,$\arcsin$ 后面的值接近于 0,而 $\arcsin$ 函数在这一点附近的变化率较小,所以会比直接用球面余弦公式来得更精确。不过也可以反过来推测,haversine 公式在两点相对的情况下(例如南北两极)误差会变大。下面就此进行测试,给出赤道上两点的经纬度,用这两个公式分别计算圆心角,比较它们与理论值之间的差异。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
from scipy.ndimage import gaussian_filter1d
def cosine(lon1, lat1, lon2, lat2):
'''利用球面余弦公式计算两点间的圆心角.'''
lon1, lat1, lon2, lat2 = map(np.deg2rad, [lon1, lat1, lon2, lat2])
dlon = lon2 - lon1
a = np.sin(lat1) * np.sin(lat2)
b = np.cos(lat1) * np.cos(lat2) * np.cos(dlon)
dtheta = np.arccos(a + b)
return np.rad2deg(dtheta)
def hav(x):
'''计算半正矢函数.'''
return np.sin(x / 2)**2
def haversine(lon1, lat1, lon2, lat2):
'''利用haversine公式计算两点间的圆心角.'''
lon1, lat1, lon2, lat2 = map(np.deg2rad, [lon1, lat1, lon2, lat2])
dlon = lon2 - lon1
dlat = lat2 - lat1
a = hav(dlat)
b = np.cos(lat1) * np.cos(lat2) * hav(dlon)
dtheta = 2 * np.arcsin(np.sqrt(a + b))
return np.rad2deg(dtheta)
if __name__ == '__main__':
npt = 10000
# 点1的经度为-180°,点2的经度范围为[-180°, 180°].
lon1 = np.full(npt, -180)
lat1 = np.zeros(npt)
lon2 = np.linspace(-180, 180, npt + 2)[1:-1] # 避开0°夹角.
lat2 = np.zeros(npt)
# 计算理论的圆心角,和两种公式导出的圆心角.
dlon = np.abs(lon2 - lon1)
deg_tru = np.where(dlon > 180, 360 - dlon, dlon)
deg_cos = cosine(lon1, lat1, lon2, lat2)
deg_hav = haversine(lon1, lat1, lon2, lat2)
# 计算与理论值之间的误差.
err_cos = np.abs(deg_cos - deg_tru) / deg_tru * 100
err_hav = np.abs(deg_hav - deg_tru) / deg_tru * 100
# 对结果进行平滑.
err_cos = gaussian_filter1d(err_cos, sigma=3)
err_hav = gaussian_filter1d(err_hav, sigma=3)
# 画图.
fig, ax = plt.subplots()
ax.plot(dlon, err_cos, lw=1, label='cosine')
ax.plot(dlon, err_hav, lw=1, label='haversine')
leg = ax.legend(frameon=False)
for line in leg.get_lines():
line.set_linewidth(2)
# 设置x轴.
ax.set_xlabel('Longitude Difference (°)', fontsize='large')
ax.set_xlim(-10, 370)
ax.xaxis.set_major_locator(mticker.MultipleLocator(60))
ax.xaxis.set_minor_locator(mticker.AutoMinorLocator(2))
# y轴采用对数坐标.
ax.set_ylabel('Deviation (%)', fontsize='large')
ax.set_yscale('log')
ax.set_ylim(1E-13, None)
ax.grid(ls='--')
plt.show()
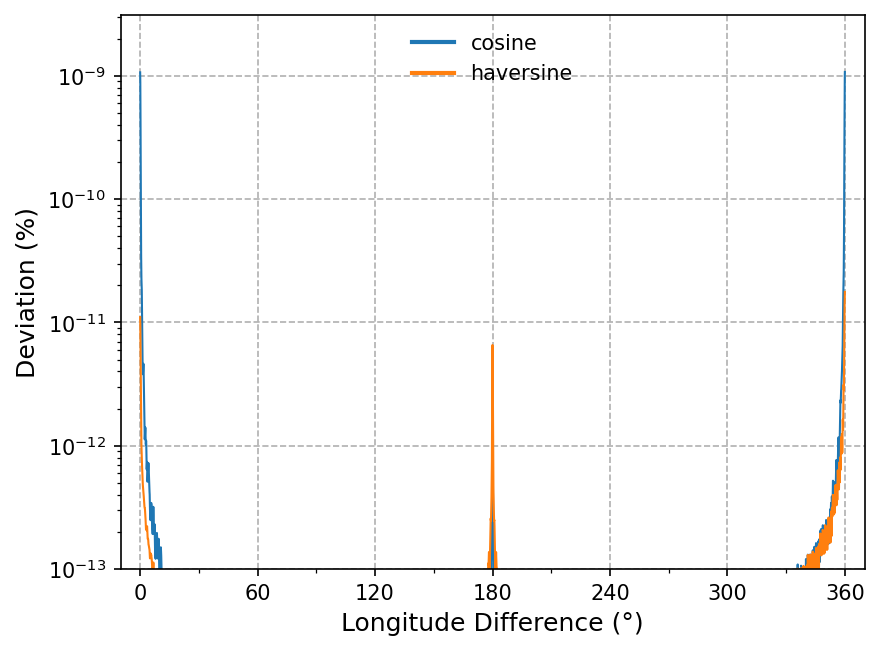
当两点间夹角接近于 0° 时,如图中最左边和最右边所示,球面余弦公式的误差大于 haversine 公式;当两点近乎相对时,如图正中间所示,haversine 公式的误差大于球面余弦公式。一个奇怪的地方是,haversine 公式在两点间夹角趋于 0° 时的误差还要略大于两点相对的情况,我也想不出原因,也许跟计算 $\Delta \phi$ 时产生的舍入误差有关?不知道有没有读者能予以解答。但总地看来,在 64 位浮点精度下这两个公式的误差完全可以忽略,实际使用时任选其一即可。如果想要现成的 haversine 公式实现,可以调用 scikit-learn 包里的 sklearn.metrics.pairwise.haversine_distances 函数。
此外维基上还提到了一个所谓球体情况下的 Vincenty 公式,声称这个公式对于任意位置的两点都精确。但我测试后发现结果比较离谱,计算出了负的圆心角,并且也可以通过数学证明这个公式是错的,所以请读者小心引用。
椭球上两点间的距离
比球体近似更精确的是椭球近似,椭球上两点距离的计算一般采用 Vincenty 公式,这是一种精度很高的迭代法,具体分为两种
- direct method:已知一点的坐标,给出朝向另一点的距离和方位角,用公式计算出另一点的坐标。
- inverse method:已知两点的坐标,用公式计算出两点间的距离和方位角。
显然我们这里需要的是 inverse method,即根据两点坐标逆向求解它们之间的距离。维基上的相关公式还有点复杂,我也不懂具体原理,所以这里就直接调包了。Python 中的 pyproj 包提供对地理坐标的变换操作,其中 Geod 类可以生成一个代表地球椭球体的对象,利用其 inv 方法即可实现 inverse method
from pyproj import Geod
# 海口的经纬度.
lon1, lat1 = 110.33, 20.07
# 北京的经纬度.
lon2, lat2 = 116.40, 39.91
# 生成一个球体,默认半径R=6370997.0m
g1 = Geod(ellps='sphere')
# 生成一个WGS84坐标系下的椭球.
g2 = Geod(ellps='WGS84')
# 计算WGS84椭球上两点之间的方位角和距离,默认经纬度单位为degree.
az12, az21, dist = g2.inv(lon1, lat1, lon2, lat2)
例如上面计算出海口到北京的距离为 2274.54 km,而球面余弦公式和 haversine 公式对这个结果的误差为 0.27 %。光看数字可能不太形象,那假设高铁时速为 250 km/h,再考虑途中有弯弯绕绕,这个距离需要坐上十几个小时的高铁。不过如第一节所述,计算出的距离会根据我们选取的地球椭球体的变化而发生变化,并且很难说哪个椭球的结果就更精确——它们都是对大地水准面的有效近似,只不过在不同区域的表现不同罢了。
Python 中的 GeoPy 包也提供类似的距离计算功能,有兴趣的读者可以试试看。
参考资料
Wikipedia: Great-circle distance