简介
连通域标记(connected component labelling)即找出二值图像中互相独立的各个连通域并加以标记,如下图所示(引自 MarcWang 的 Gist)
可以看到图中有三个独立的区域,我们希望找到并用数字标记它们,以便计算各个区域的轮廓、外接形状、质心等参数。连通域标记最基本的两个算法是 Seed-Filling 算法和 Two-Pass 算法,下面便来分别介绍它们,并用 Python 加以实现。
(2022-01-04 更新:修复了 seed_filling 重复追加相邻像素的问题,修改了其它代码的表述。)
Seed-Filling 算法
直译即种子填充,以图像中的特征像素为种子,然后不断向其它连通区域蔓延,直至将一个连通域完全填满。示意动图如下(引自 icvpr 的博客)

具体思路为:循环遍历图像中的每一个像素,如果某个像素是未被标记过的特征像素,那么用数字对其进行标记,并寻找与之相邻的未被标记过的特征像素,再对这些像素也进行标记,然后以同样的方法继续寻找与这些像素相邻的像素并加以标记……如此循环往复,直至将这些互相连通的特征像素都标记完毕,此即连通域 1。接着继续遍历图像像素,看能不能找到下一个连通域。下面的实现采用深度优先搜索(DFS)的策略:将与当前位置相邻的特征像素压入栈中,弹出栈顶的像素,再把与这个像素相邻的特征像素压入栈中,重复操作直至栈内像素清空。
import numpy as np
def seed_filling(image, diag=False):
'''
用Seed-Filling算法标记图片中的连通域.
Parameters
----------
image : ndarray, shape (nrow, ncol)
图片数组,零值表示背景,非零值表示特征.
diag : bool
指定邻域是否包含四个对角.
Returns
-------
labelled : ndarray, shape (nrow, ncol), dtype int
表示连通域标签的数组,0表示背景,从1开始表示标签.
nlabel : int
连通域的个数.
'''
# 用-1表示未被标记过的特征像素.
image = np.asarray(image, dtype=bool)
nrow, ncol = image.shape
labelled = np.where(image, -1, 0)
# 指定邻域的范围.
if diag:
offsets = [
(-1, -1), (-1, 0), (-1, 1),(0, -1),
(0, 1), (1, -1), (1, 0), (1, 1)
]
else:
offsets = [(-1, 0), (0, -1), (0, 1), (1, 0)]
def get_neighbor_indices(row, col):
'''获取(row, col)位置邻域的下标.'''
for (dx, dy) in offsets:
x = row + dx
y = col + dy
if 0 <= x < nrow and 0 <= y < ncol:
yield x, y
label = 1
for row in range(nrow):
for col in range(ncol):
# 跳过背景像素和已经标记过的特征像素.
if labelled[row, col] != -1:
continue
# 标记当前位置和邻域内的特征像素.
current_indices = []
labelled[row, col] = label
for neighbor_index in get_neighbor_indices(row, col):
if labelled[neighbor_index] == -1:
labelled[neighbor_index] = label
current_indices.append(neighbor_index)
# 不断寻找与特征像素相邻的特征像素并加以标记,直至再找不到特征像素.
while current_indices:
current_index = current_indices.pop()
labelled[current_index] = label
for neighbor_index in get_neighbor_indices(*current_index):
if labelled[neighbor_index] == -1:
labelled[neighbor_index] = label
current_indices.append(neighbor_index)
label += 1
return labelled, label - 1
Two-Pass 算法
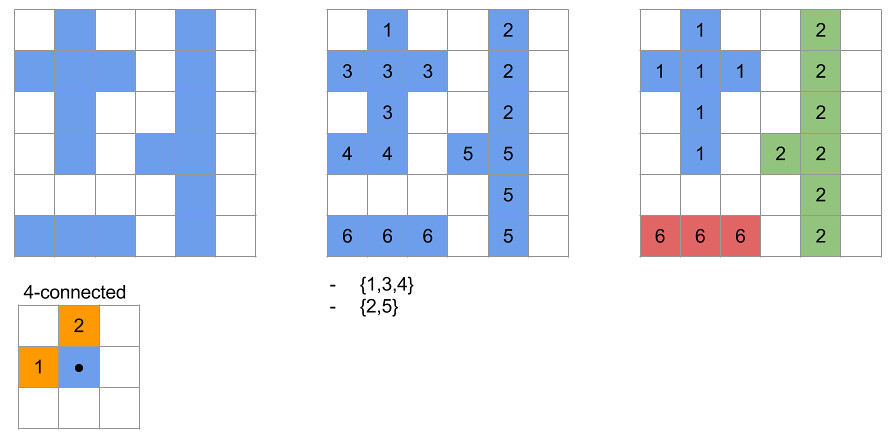
顾名思义,是会对图像过两遍循环的算法。第一遍循环先粗略地对特征像素进行标记,第二遍循环中再根据不同标签之间的关系对第一遍的结果进行修正。示意动图如下(引自 icvpr 的博客)

具体思路为
- 第一遍循环时,若一个特征像素周围全是背景像素,那它很可能是一个新的连通域,需要赋予其一个新标签。如果这个特征像素周围有其它特征像素,则说明它们之间互相连通,此时随便用它们中的一个旧标签值来标记当前像素即可,同时要用并查集记录这些像素的标签间的关系。
- 因为我们总是只利用了当前像素邻域的信息(考虑到循环方向是从左上到右下,邻域只需要包含当前像素的上一行和本行的左边),所以第一遍循环中找出的那些连通域可能会在邻域之外相连,导致同一个连通域内的像素含有不同的标签值。不过利用第一遍循环时获得的标签之间的关系(记录在并查集中),可以在第二遍循环中将同属一个集合(连通域)的不同标签修正为同一个标签。
- 经过第二遍循环的修正后,虽然假独立区域会被归并,但它所持有的标签值依旧存在,这就导致本应连续的标签值序列中有缺口(gap)。所以依据需求可以进行第三遍循环,去掉这些缺口,将标签值修正为连续的整数序列。
其中提到的并查集是一种处理不相交集合的数据结构,支持查询元素所属、合并两个集合的操作。利用它就能处理标签和连通域之间的从属关系。我是看 算法学习笔记(1) : 并查集 这篇知乎专栏学的。下面的实现中仅采用路径压缩的优化,合并两个元素时始终让大的根节点被合并到小的根节点上,以保证连通域标签值的排列顺序跟数组的循环方向一致。
from scipy.stats import rankdata
class UnionFind:
'''用列表实现简单的并查集.'''
def __init__(self, n):
'''创建含有n个节点的并查集,每个元素指向自己.'''
self.parents = list(range(n))
def find(self, i):
'''递归查找第i个节点的根节点,同时压缩路径.'''
parent = self.parents[i]
if parent == i:
return i
else:
root = self.find(parent)
self.parents[i] = root
return root
def union(self, i, j):
'''合并节点i和j所属的两个集合.保证大的根节点被合并到小的根节点上.'''
root_i = self.find(i)
root_j = self.find(j)
if root_i < root_j:
self.parents[root_j] = root_i
elif root_i > root_j:
self.parents[root_i] = root_j
else:
return None
def two_pass(image, diag=False):
'''
用Two-Pass算法标记图片中的连通域.
Parameters
----------
image : ndarray, shape (nrow, ncol)
图片数组,零值表示背景,非零值表示特征.
diag : bool
指定邻域是否包含四个对角.
Returns
-------
labelled : ndarray, shape (nrow, ncol), dtype int
表示连通域标签的数组,0表示背景,从1开始表示标签.
nlabel : int
连通域的个数.
'''
image = np.asarray(image, dtype=bool)
nrow, ncol = image.shape
labelled = np.zeros_like(image, dtype=int)
uf = UnionFind(image.size // 2)
# 指定邻域的范围,相比seed-filling只有半边.
if diag:
offsets = [(-1, -1), (-1, 0), (-1, 1), (0, -1)]
else:
offsets = [(-1, 0), (0, -1)]
def get_neighbor_indices(row, col):
'''获取(row, col)位置邻域的下标.'''
for (dx, dy) in offsets:
x = row + dx
y = col + dy
if 0 <= x < nrow and 0 <= y < ncol:
yield x, y
label = 1
for row in range(nrow):
for col in range(ncol):
# 跳过背景像素.
if not image[row, col]:
continue
# 寻找邻域内特征像素的标签.
feature_labels = []
for neighbor_index in get_neighbor_indices(row, col):
neighbor_label = labelled[neighbor_index]
if neighbor_label > 0:
feature_labels.append(neighbor_label)
# 当前位置取邻域内的标签,同时记录邻域内标签间的关系.
if feature_labels:
first_label = feature_labels[0]
labelled[row, col] = first_label
for feature_label in feature_labels[1:]:
uf.union(first_label, feature_label)
# 若邻域内没有特征像素,当前位置获得新标签.
else:
labelled[row, col] = label
label += 1
# 获取所有集合的根节点,由大小排名得到标签值.
roots = [uf.find(i) for i in range(label)]
labels = rankdata(roots, method='dense') - 1
# 利用advanced indexing替代循环修正标签数组.
labelled = labels[labelled]
return labelled, labelled.max()
其中对标签值进行重新排名的部分用到了 scipy.stats.rankdata 函数,自己写循环来实现也可以,但当标签值较多时效率会远低于这个函数。从代码来看,Two-Pass 算法比 Seed-Filling 算法更复杂一些,但因为不需要进行递归式的填充,所以理论上要比后者更快。
其它方法
许多图像处理的包里有现成的函数,例如
scipy.ndimage.labelskimage.measure.labelcv2.connectedComponets
具体信息和用法请查阅文档。顺便测一下各方法的速度,如下图所示(通过 IPython 的 %timeit 测得)

显然调包要比手工实现快 100 倍,这是因为 scipy.ndimage.label 和 skimage.measure.label 使用了更高级的算法和 Cython 代码。因为我不懂 OpenCV,所以这里没有展示 cv2.connectedComponets 的结果。
值得注意的是,虽然上一节说理论上 Two-Pass 算法比 Seed-Filling 快,但测试结果相差不大,这可能是由于纯 Python 实现体现不出二者的差异(毕竟完全没用到 NumPy 数组的向量性质),也可能是我代码写的太烂,还请懂行的读者指点一下。
例子
以一个随机生成的 (50, 50) 的二值数组为例,展示 scipy.ndimage.label、seed_filling 和 two_pass 三者的效果,采用 8 邻域连通,如下图所示

可以看到三种方法都找出了 17 个连通域,并且连标签顺序都一模一样(填色相同)。不过若 Two-Pass 法中的并查集采用其它合并策略,标签顺序就很可能发生变化。下面再以一个更复杂的 (800, 800) 大小的空露露图片为例

将图片二值化后再进行连通域标记,可以看到おつるる的字样被区分成多个区域,猫猫和露露也都被识别了出来。代码如下
import numpy as np
from PIL import Image
from scipy import ndimage
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from connected_components import two_pass, seed_filling
if __name__ == '__main__':
# 将测试图片二值化.
picname = 'ruru.png'
image = Image.open(picname)
image = np.array(image.convert('L'))
image = ndimage.gaussian_filter(image, sigma=2)
image = np.where(image < 220, 1, 0)
# 设置二值图像与分类图像所需的cmap.
cmap1 = mcolors.ListedColormap(
['white', 'black'])
white = np.array([1, 1, 1])
cmap2 = mcolors.ListedColormap(
np.vstack([white, plt.cm.tab20.colors])
)
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
# 关闭ticks的显示.
for ax in axes.flat:
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
# 显示二值化的图像.
axes[0, 0].imshow(image, cmap=cmap1, interpolation='nearest')
axes[0, 0].set_title('Image', fontsize='large')
# 显示scipy.ndimage.label的结果.
# 注意imshow中需要指定interpolation为'nearest'或'none',否则结果有紫边.
s = np.ones((3, 3), dtype=int)
labelled, nlabel = ndimage.label(image, structure=s)
axes[0, 1].imshow(labelled, cmap=cmap2, interpolation='nearest')
axes[0, 1].set_title(
f'scipy.ndimage.label ({nlabel} labels)', fontsize='large'
)
# 显示Two-Pass算法的结果.
labelled, nlabel = two_pass(image, diag=True)
axes[1, 0].imshow(labelled, cmap=cmap2, interpolation='nearest')
axes[1, 0].set_title(f'Two-Pass ({nlabel} labels)', fontsize='large')
# 显示Seed-Filling算法的结果.
labelled, nlabel = seed_filling(image, diag=True)
axes[1, 1].imshow(labelled, cmap=cmap2, interpolation='nearest')
axes[1, 1].set_title(f'Seed-Filling ({nlabel} labels)', fontsize='large')
fig.savefig('image.png', dpi=200, bbox_inches='tight')
plt.close(fig)
不只是邻接
虽然 scipy.ndimage.label 和 skimage.measure.label 要比手工实现更快,但它们都只支持 4 邻域和 8 邻域的连通规则,而手工实现还可以采用别的连通规则。例如,改动一下 seed_filling 中关于 offsets 的部分,使之能够表示以当前像素为原点,r 为半径的圆形邻域
offsets = []
for i in range(-r, r + 1):
k = r - abs(i)
for j in range(-k, k + 1):
offsets.append((i, j))
offsets.remove((0, 0)) # 去掉原点.
在某些情况下也许能派上用场。
参考链接
网上很多教程抄了这篇,但里面 Two-Pass 算法的代码里不知道为什么没用并查集,可能会有问题。
OpenCV_连通区域分析(Connected Component Analysis-Labeling)
一篇英文的对 Two-Pass 算法的介绍,Github 上还带有 Python 实现。
代码参考了