搞颜色系列：单色光光谱

前言

人眼可见色域在色度图中表现为彩色的马蹄形，单色光（monochromatic light）的颜色对应于马蹄的弧形边界。本文想将单色光的颜色按波长线性增大的顺序一字排开，用类似彩虹渐变图的形式展示单色光光谱。用 Python 的 Matplotlib 包来实现的话，很快就能决定画图思路：

读取 XYZ 颜色匹配函数（CMF）作为 XYZ 三刺激值。
XYZ 变换为 sRGB，接着做 gamma 校正。
用 RGB 数组构造 ListedColormap 对象，用 plt.colorbar 画出。

RGB 要求范围在 $[0, 1]$，但 CMF 直接计算出的 RGB 既有负数分量，也有大于 1 的分量，所以必须采用一种方法处理范围外的分量。最后的画图效果会因处理方法的不同产生很大差别，例如下图的三条光谱：

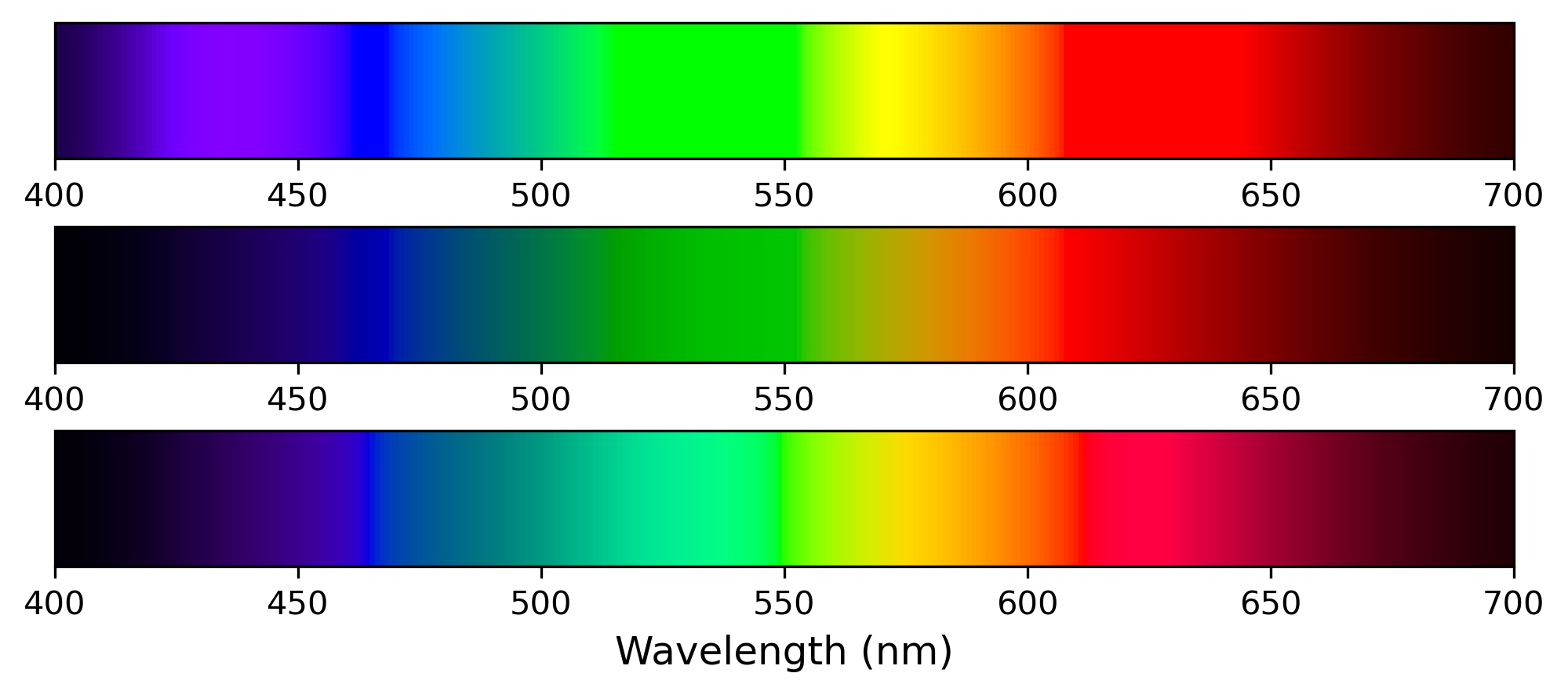
就采取了不同的处理方式，因此在发色、颜色过渡，和亮度表现上都大有不同。本文将尝试实现不同的效果并加以分析。完整代码和相关数据见我的 Github 仓库。

理论知识

本节将依次介绍 CIE RGB、XYZ 和 sRGB，以及画图时会用到的一些结论。

CIE RGB

CIE RGB 基于 700 nm 的红光、546.1 nm 的绿光，和 435.8 nm 的蓝光，CMF 指 $\bar{r}(\lambda)$、$\bar{g}(\lambda)$ 和 $\bar{b}(\lambda)$ 三条函数曲线，满足方程

$$ V(\lambda) = L_R \bar{r}(\lambda) + L_G \bar{g}(\lambda) + L_B \bar{b}(\lambda) $$

其中 $V(\lambda)$ 是光效函数（luminous efficiency function），表示相对于 555 nm 单色绿光，人眼对于波长为 $\lambda$ 的单色光的敏感度；常数 $L_R = 1$，$L_G = 4.5907$，$L_B = 0.0601$。该方程的物理意义是，颜色匹配实验中为了匹配单位辐亮度（radiance）的单色光 $\lambda$，需要辐亮度为 $L_R \bar{r}(\lambda) / V(\lambda)$ 的红光、$L_G \bar{g}(\lambda) / V(\lambda)$ 的绿光，和 $L_B \bar{b}(\lambda) / V(\lambda)$ 的蓝光。

对功率谱（power spectrum）为 $P(\lambda)$ 的任意光，定义其三刺激值（tristimulus）为

$$ \begin{gather*} R = \int \bar{r}(\lambda) P(\lambda) d\lambda \cr G = \int \bar{g}(\lambda) P(\lambda) d\lambda \cr B = \int \bar{b}(\lambda) P(\lambda) d\lambda \end{gather*} $$

该光束的颜色就由向量 $(R, G, B)$ 描述。因为光束的辐亮度和光源的功率成正比，所以三刺激值可以理解为，匹配目标光所需基色光的数量。接着介绍三条重要的性质：

CMF 可以视作功率为 1 W 的单色光的三刺激值。
三刺激值之间的比例决定颜色的色度（chromaticity）。
$L_R R + L_G G + L_B B$ 线性正比于颜色的辐亮度和视亮度（luminance）。

由性质 2 和 3 可以推论，$(kR, kG, kB)$ 意味着维持色度不变，亮度变为 $k$ 倍。

CMF 在有些波段存在负值，例如 440 到 550 nm 间的 $\bar{r}(\lambda)$，说明有些单色光无法用 CIE RGB 的三基色光混合出来，但如果先在目标光上面叠加红光，那么就能用绿光和蓝光混合出目标光，这就相当于是混合了负量的红光。同理，有些非单色光会计算出负的三刺激值。这两个事实意味着现实世界有很多颜色无法直接通过混合三基色得到。

CIE XYZ

国际照明委员会（CIE）挑选了三个不存在的假想色（imaginay colors）作为色彩空间的新基向量，对 CIE RGB 空间做线性变换得到了 CIE XYZ 空间，XYZ 空间的 CMF 是 $\bar{x}(\lambda)$、$\bar{y}(\lambda)$ 和 $\bar{z}(\lambda)$。同样定义三刺激值

$$ \begin{gather*} X = \int \bar{x}(\lambda) P(\lambda) d\lambda \cr Y = \int \bar{y}(\lambda) P(\lambda) d\lambda \cr Z = \int \bar{z}(\lambda) P(\lambda) d\lambda \end{gather*} $$

XYZ 空间的主要性质是：

CMF 全为正值，人眼可见颜色的三刺激值都是正数。
三刺激值之间的比例决定颜色的色度。
$Y = L_R R + L_G G + L_B B$

第三条意味着 $Y$ 能直接指示亮度，但若想维持色度不变修改亮度，还是需要同时缩放三刺激值。

XYZ 空间主要用于颜色的理论表示，以及作为色彩空间变换的中间量。我们平时用到的和能下载到的都是 XYZ CMF。

sRGB

显示器显示颜色要用到 sRGB，以 CRT 显示器的红绿蓝磷光体（phosphor）为色彩空间的新基向量，对 CIE XYZ 空间做线性变换得到了 sRGB 空间。类似 CIE RGB 空间，sRGB 也用 RGB 值描述颜色。最终显示前还需要做 gamma 校正，详细计算公式可见搞颜色系列：绘制 CIE 1931 色度图。接下来的讨论里提到 RGB 的地方都是指 sRGB，并且会忽略 gamma 校正环节。

sRGB 空间的主要性质是：

单色光的 RGB 都存在负数分量。
RGB 值之间的比例决定颜色的色度。
$Y = 0.2126 R + 0.7152 G + 0.072 B$
显示时要求 $R, G, B \in [0, 1]$。

性质 1 是因为色度图上单色光对应的马蹄形边界全在 sRGB 的三角形色域外，sRGB 的三基色光不能直接混合得到单色光。性质 2 和 3 直接源于 CIE RGB，同样能推论 $(kR, kG, kB)$ 表示亮度变为 $k$ 倍。性质 4 需要详细解释一下：显示器的像素不能产生负量的基色光，所以不允许分量小于 0；显示器的亮度可以通过面板上的按钮从最低档调到最高档，$(R, G, B)$ 表示的颜色在不同的亮度档位下呈现不同的亮度。所以把 RGB 看作绝对量是没有意义的，将其视为 $[0, 1]$ 之间的相对量更加便利。

实际计算时如果碰到 RGB 分量是负数的情况，可以直接将负值修改为 0；碰到大于 1 的情况，考虑到相对量的概念，可以根据需求对 RGB 整体做缩放，只要最大分量小于 1 就行。

本节关于亮度的性质主要基于个人理解，在翻阅相关教材时没看到有明确这么表述的，如果有误还请读者指出。但不管对不对，后面的画图环节马上就会用到。

画图

单色光的 RGB

需要用到的数据是伦敦大学学院 CVRL 实验室官网提供的 CIE 1931 XYZ CMF，范围从 360 到 830 nm，分辨率为 1nm。直接用 Pandas 读取：

import pandas as pd

cmf = pd.read_csv('./data/cie_1931_2deg_xyz_cmf.csv', index_col=0)

CMF 可以看作功率为 1 W 的单色光的 XYZ 值，根据 XYZ 到 sRGB 的变换公式

$$ \begin{bmatrix} R \cr G \cr B \end{bmatrix} = \begin{bmatrix} +3.2406 & -1.5372 & -0.4986 \cr -0.9689 & +1.8758 & +0.0415 \cr +0.0557 & -0.2040 & +1.0570 \end{bmatrix} \begin{bmatrix} X \cr Y \cr Z \end{bmatrix} $$

import numpy as np

XYZ = cmf.to_numpy()
Y = XYZ[:, 1]

M = np.array([
    [+3.2406, -1.5372, -0.4986],
    [-0.9689, +1.8758, +0.0415],
    [+0.0557, -0.2040, +1.0570]
])
RGB = np.tensordot(XYZ, M, (-1, 1))

CMF 的 RGB 和 $Y$ 曲线如下图所示：

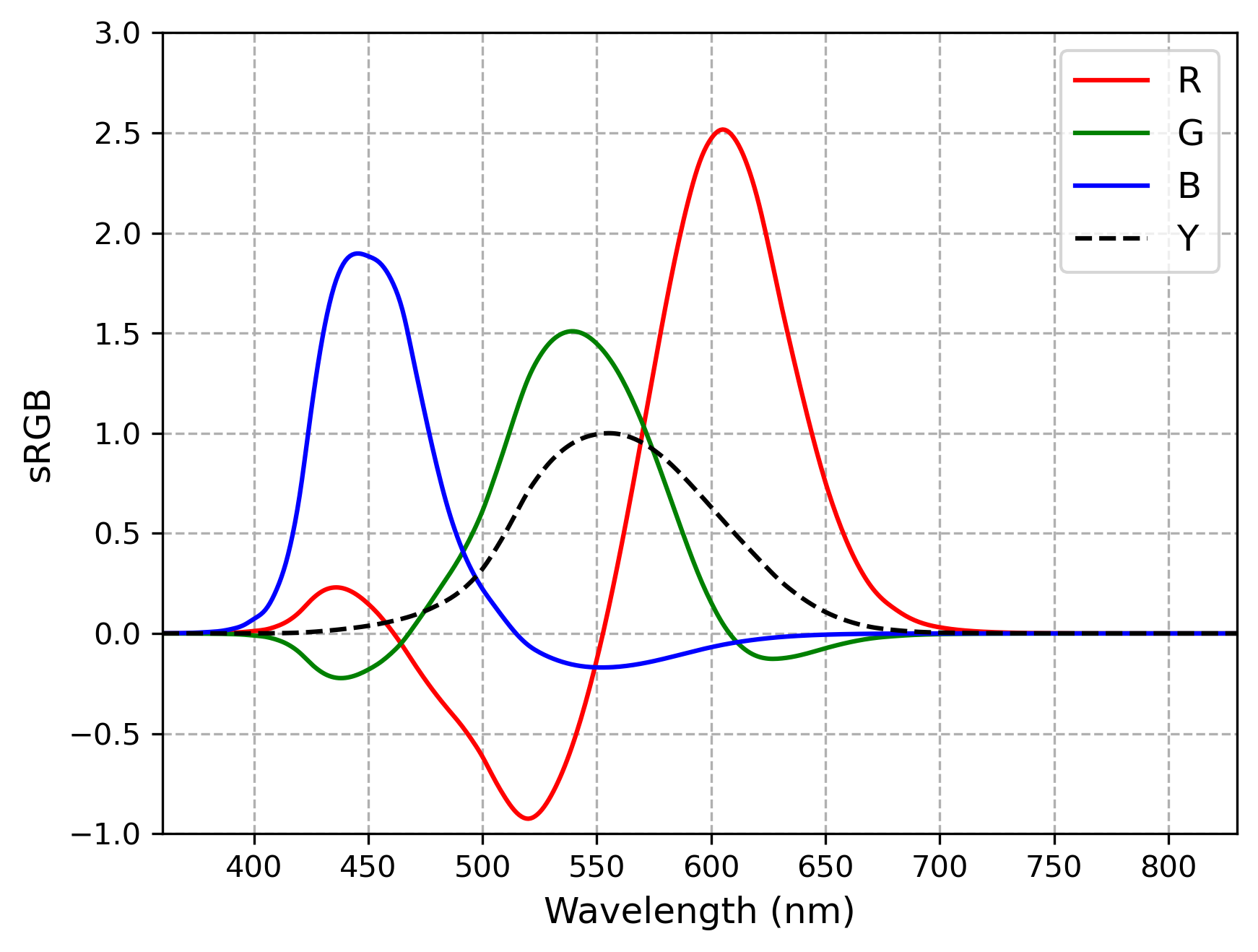
cmf_rgb

如上一节所述，RGB 全波段都存在负数分量，有些波段的分量大于 1。$Y$ 曲线实际上就是 $V(\lambda)$，最高点是 555 nm 绿光处，亮度向短波和长波端递减至 0。画光谱时必须将分量处理到 $[0, 1]$ 范围内，下面测试不同处理方法的效果。

方法一：clip

最朴素的做法是用 np.clip 函数将负数修改为 0，大于 1 的数修改为 1：

RGB = RGB.clip(0, 1)

光谱颜色用 plt.colorbar 画出：

import matplotlib.pyplot as plt
from matplotlib.colors import Normalize, ListedColormap
from matplotlib.cm import ScalarMappable
from matplotlib.ticker import MultipleLocator

fig, ax = plt.subplots(figsize=(8, 1))
mappable = ScalarMappable(
    norm=Normalize(*cmf.index[[0, -1]]),
    cmap=ListedColormap(gamma_encoding(RGB))
)
cbar = fig.colorbar(mappable, cax=ax, orientation='horizontal')
cbar.set_ticks(MultipleLocator(50))

为了便于分析，额外画出处理后的 RGB 和反算出来的 $Y$，以及色度图上处理前的单色光颜色，处理后会被映射到什么颜色上：

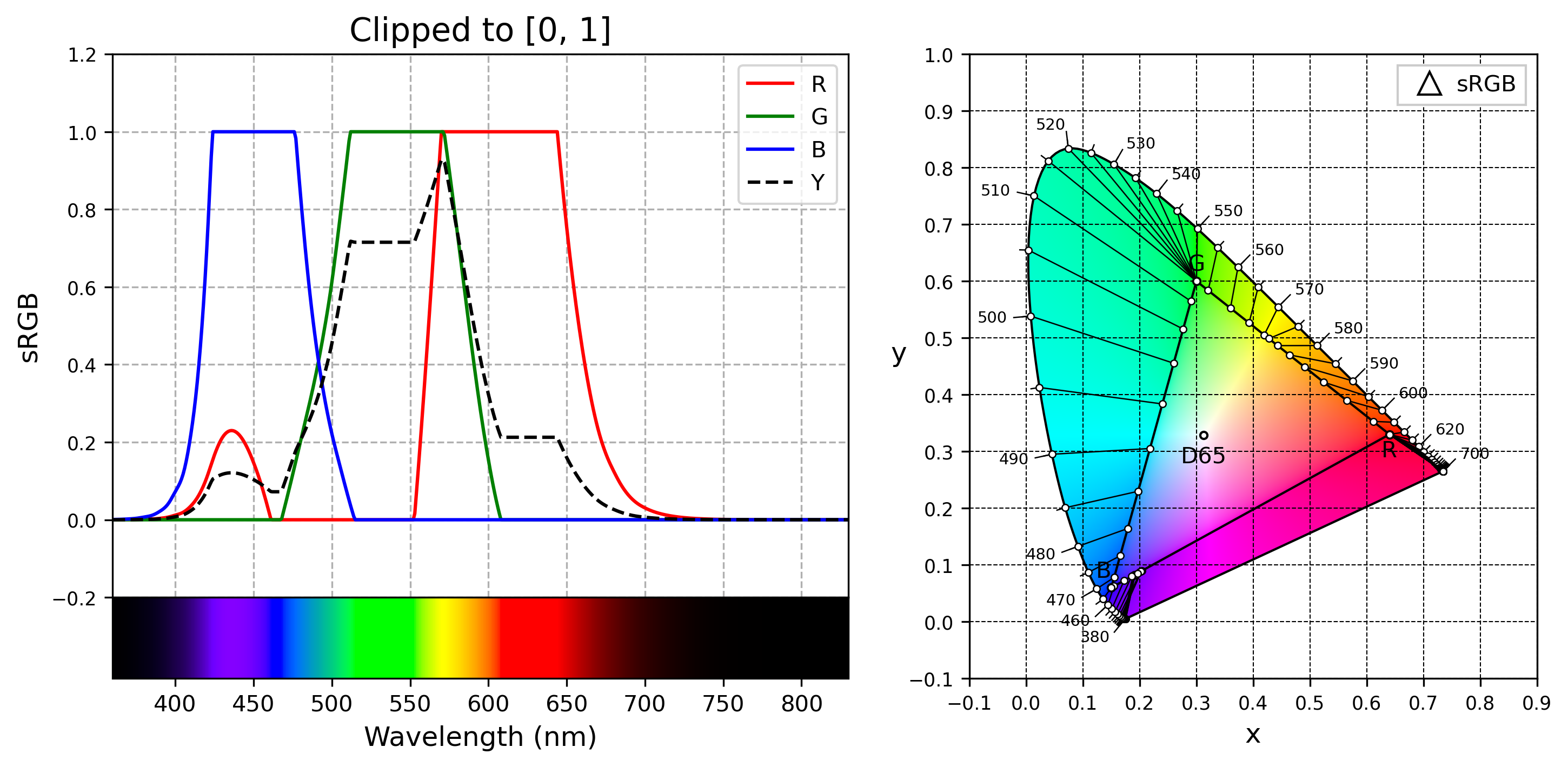
先看左下角的光谱：

410 - 455 nm 呈红紫色（purple），比右边的蓝色还亮。
蓝色、绿色和红色区域内缺乏过渡，以 510 - 560 nm 为例，看起来像是同一种绿色绿了一片。

这些问题都可以用左上的曲线图解释：

410 - 455 nm 波段的紫色本来应该由蓝色、红色，和负量的绿色混合得到，现在 $G = 0$，所以呈红紫色；由 $Y = 0.2126 R + 0.7152 G + 0.072 B$，$G = 0$ 相当于增大 $Y$，所以 $Y$ 曲线在这一段凸起，比右边的蓝色更亮。
510 - 560 nm 波段负数 $R$ 和 $B$ 变成 0，本来大于 1 且有变化的 $G$ 全变成 1，所以这一段全是 $(0, 1, 0)$ 的绿色。同理 600 - 650 nm 全是 $(1, 0, 0)$ 的红色。

右边的映射图也能给出形象的解释：边界上 505 - 550 nm 的颜色全被映射到了 sRGB 三角的 $G$ 顶点上，同理 610 - 800 nm 的颜色全被映射到了 $R$ 顶点上。

方法二：压缩高度

第二个方法是先用 clip 去除负数分量，再同时压缩三条 RGB 曲线直到最高点恰好为 1：

RGB = RGB.clip(0, None)
RGB /= RGB.max()

其中 RGB.max() 对应于 $R(605 ; \rm{nm}) = 2.517$。效果如下图：

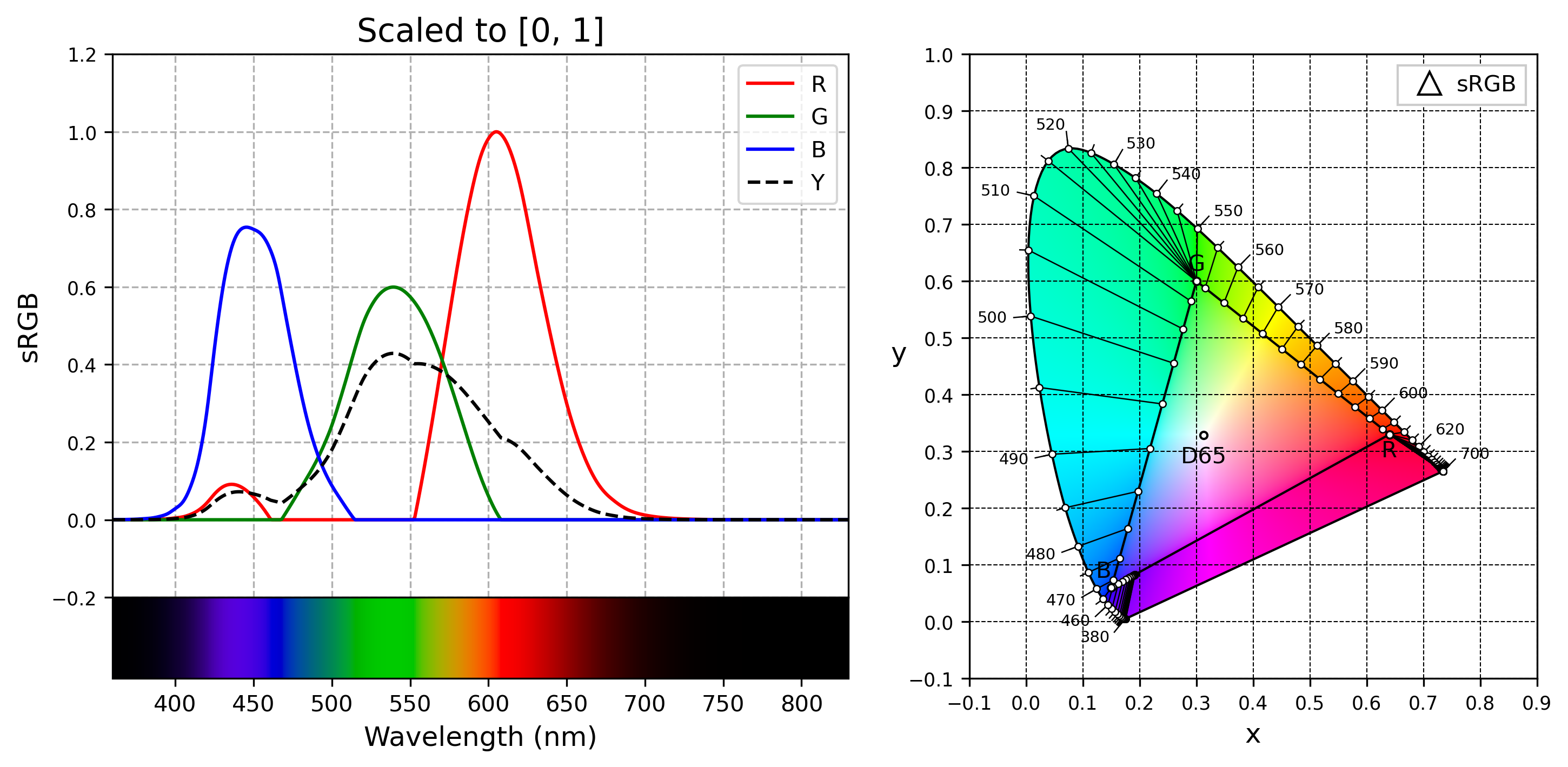
相比方法一：

因为 RGB 整体除以 2.517，所以 $Y$ 曲线的高度下降，导致光谱亮度仅有方法一的一半，黄色因为太暗显得发棕。
410 - 455 nm 的紫色亮度依旧比周围高，但没有方法一那么明显了。
蓝色、绿色和红色部分现在有了平滑的过渡。
色度图上短波和长波端的颜色映射相比方法一稍有区别。

方法三：调整亮度

紫色偏亮的问题可以通过调整亮度解决：

设 CMF 的亮度为 $Y_1$。
CMF 变换为 RGB 后用 clip 去除负数分量，再变换回 XYZ 值，得到亮度 $Y_2$。
RGB 乘以 $Y_1 / Y_2$。
RGB 曲线压缩至最高高度为 1。

最后得到的 $Y$ 曲线的形状和 $V(\lambda)$ 相同，但高度有压缩。代码为：

Y1 = XYZ[:, 1]
RGB = RGB.clip(0, None)
Y2 = sRGB_to_XYZ(RGB)[:, 1]
RGB *= Y1 / Y2
RGB /= RGB.max()

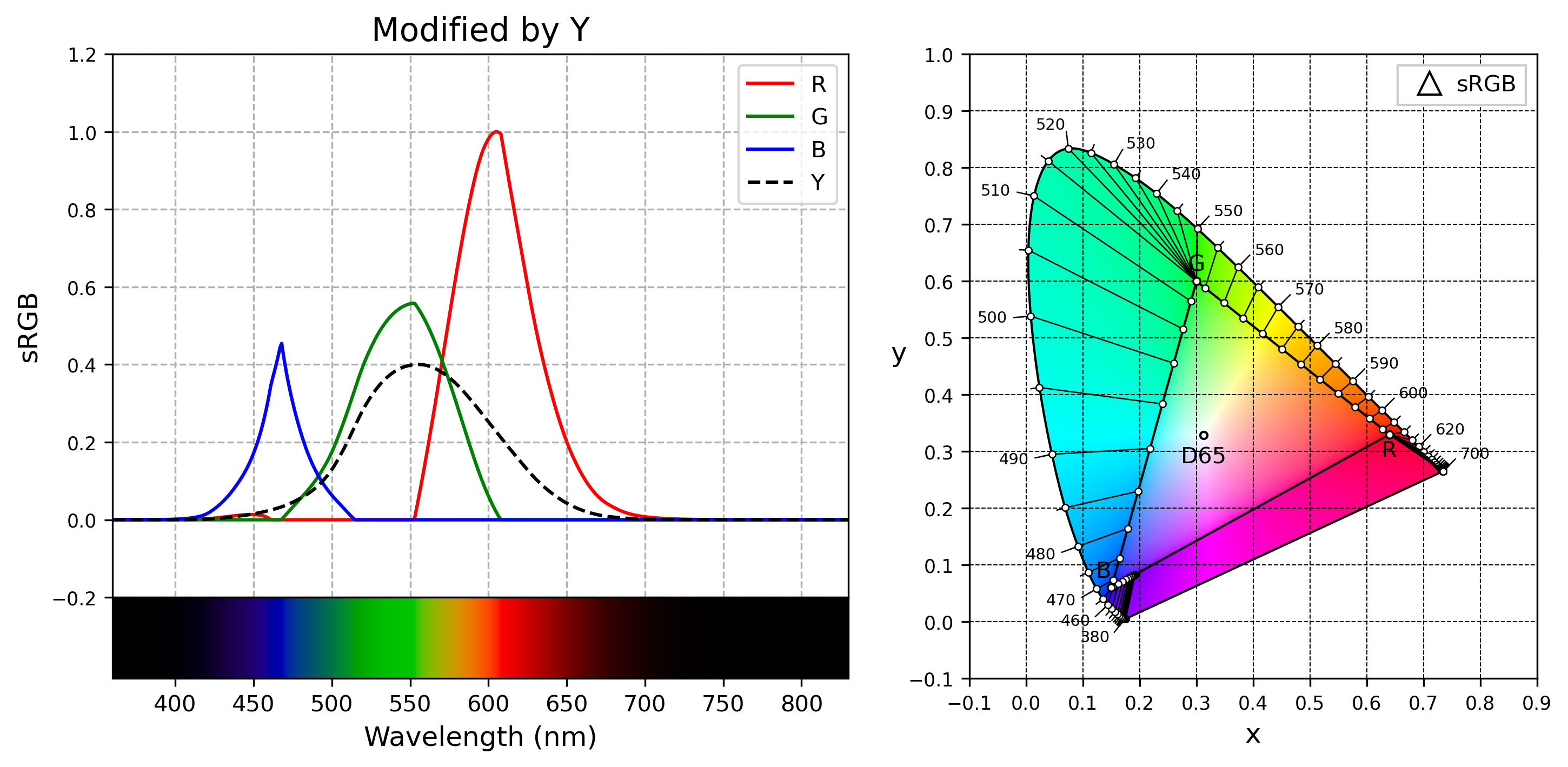
观感和方法二非常接近，但紫色不再偏亮。

方法四：沿连线朝白色移动

色度图上让单色光的颜色沿直线向 sRGB 的白点移动，RGB 的负数分量会逐渐增大，到达 sRGB 的三角形色域边界时恰好为 0，取交点处的颜色作为单色光颜色的近似。相比于 clip 方法，该方法的色相（hue）与原单色光更接近，但饱和度（saturation）会更低。搞颜色系列：绘制 CIE 1931 色度图中已经论述过，如果一个颜色的最小分量为负数，那么让每个分量都减去这个负数即可。明确一下方法四的流程：

CMF 变换得到 RGB。
每个颜色的 RGB 减去最小的负数分量。
RGB 乘以 $Y_1 / Y_2$ 调整亮度。
RGB 曲线压缩至最高高度为 1。

Y1 = XYZ[:, 1]
RGB -= RGB.min(axis=1, keepdims=True).clip(None, 0)
Y2 = sRGB_to_XYZ(RGB)[:, 1]
RGB *= Y1 / Y2
RGB /= RGB.max()

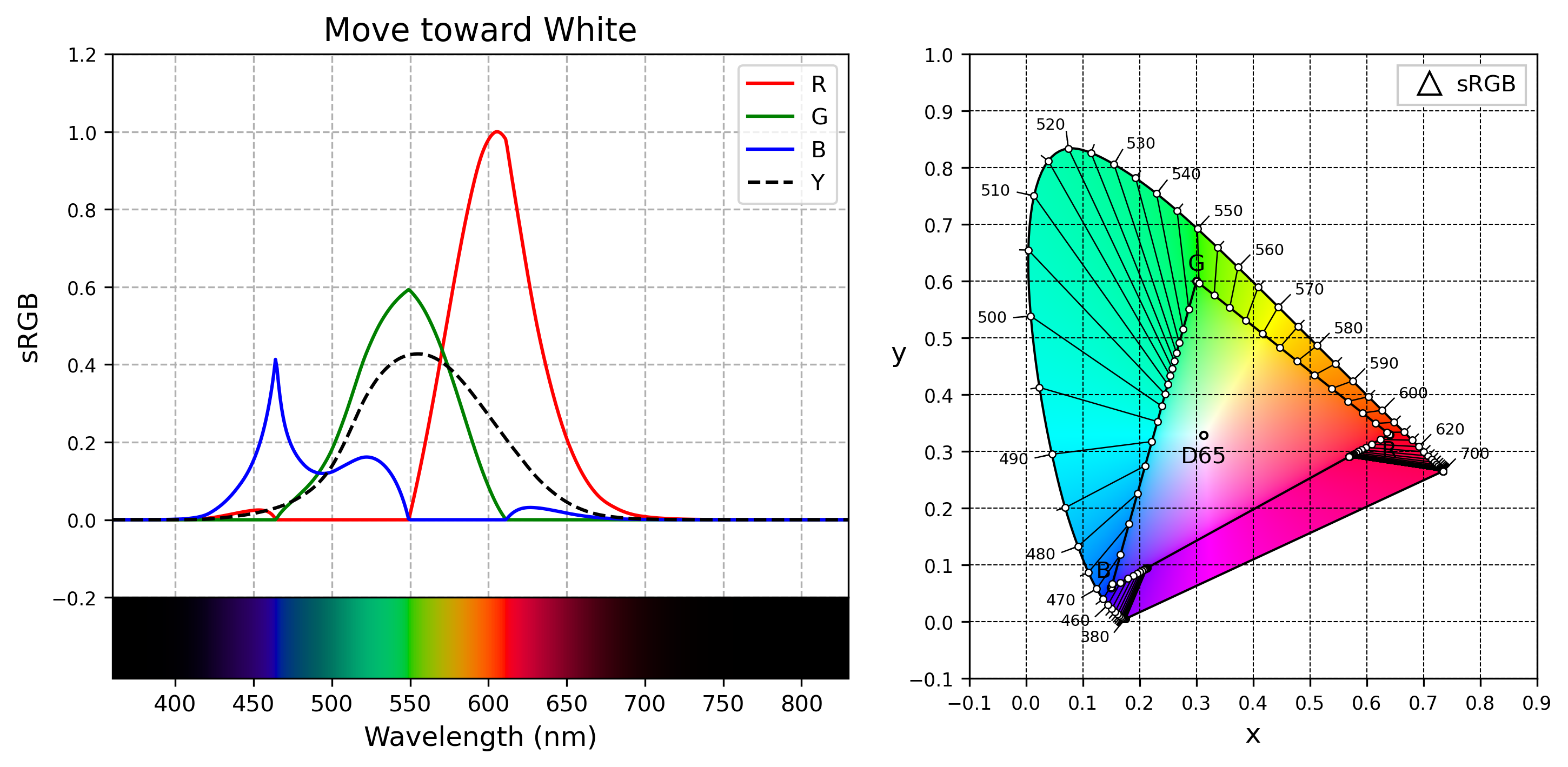
前几种方法里 510 - 540 nm 的绿色都映射到色度图上的 $G$ 顶点附近，而方法四里这一波段的绿色都映射到了 $GB$ 直线上，表现出蓝绿混合的青色（cyan），只不过因为饱和度低显得不是很纯净。另外曲线图里 $B$ 变成了很搞笑的形状。

颜色增亮

方法三和四都比直接 clip 的方法一看起来更自然，无奈因为 RGB /= RGB.max() 操作亮度减半，看起来像是蒙了一层灰脏兮兮的。所以最后决定整体放大 RGB 来增亮，这里以方法四为例，参考 Rendering Spectra 选择 1.8 的倍数：

RGB *= 1.8
RGB = RGB.clip(0, 1)

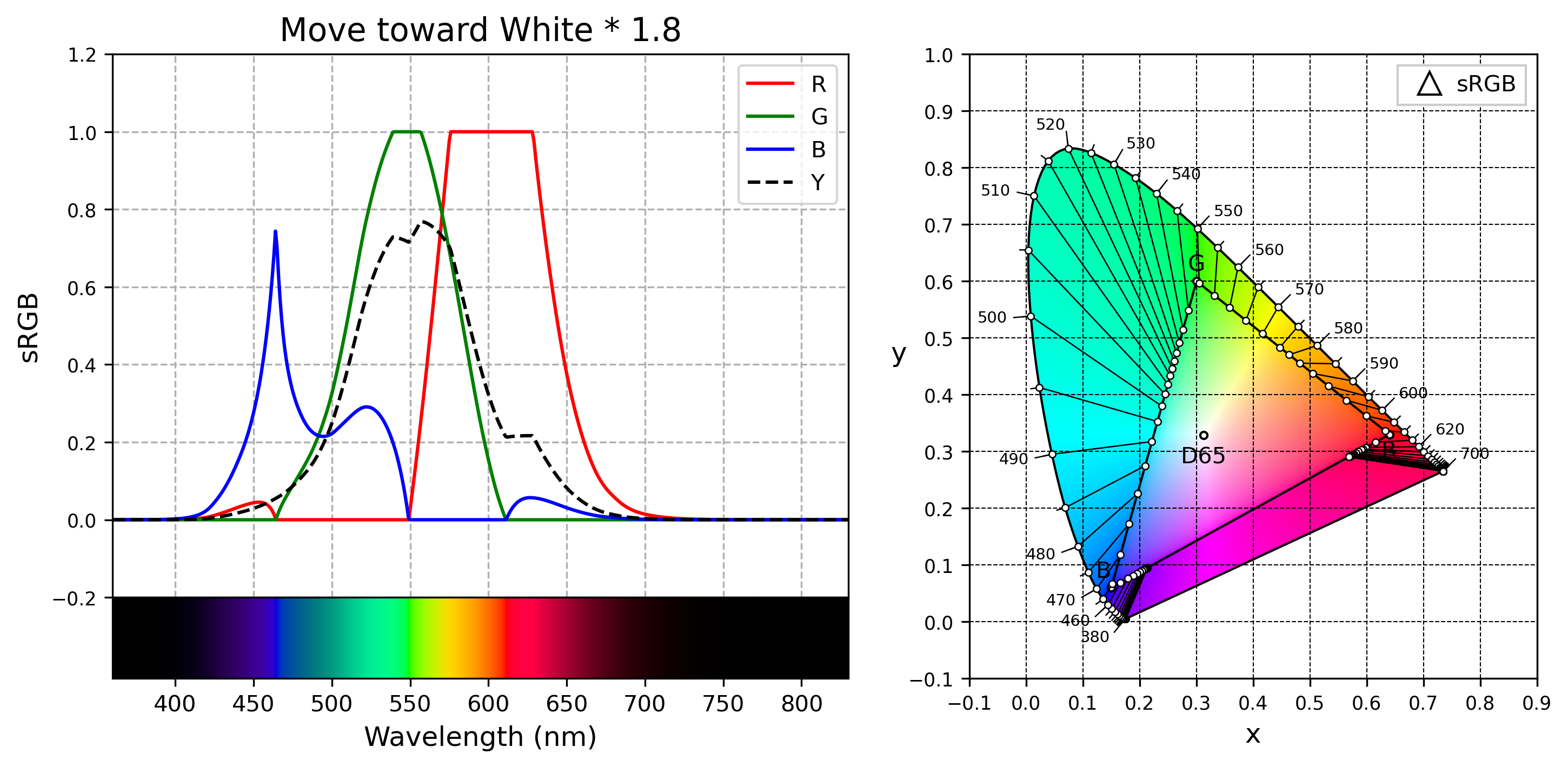
这下看起来靓丽多了。但是 $R$ 和 $G$ 超过 1 的部分需要做 clip，所以 610 - 630 nm 的红色区域又有点红成一片的效果，不过比方法一还是轻微许多，可以接受。

当然除了整体增亮以外，还有一种简单粗暴的方式，那就是调高屏幕亮度……

结语

本文开头的三条光谱，分别对应于方法一（clip）、方法三（调整亮度）和方法四（沿连线朝白色移动，再增亮 1.8 倍）。

Python Colour 包的 plot_visible_spectrum 函数能直接画出单色光光谱，默认效果非常接近本文的方法二，整体略暗，紫色发亮。所以本文有助于解释为什么调包画出来是那样一种效果，以及如何自己实现其它效果。另外网上直接搜索 “visible light spectrum” 的图片，会发现大部分图片里光谱里蓝绿之间的青色非常明显，蓝色段也很宽。我现在还没想到这个效果是怎么做到的，如果有读者了解还请指教。

参考资料

Color Vision and Colorimetry: Theory and Applications, Second Edition

Convert light frequency to RGB?

Colour Rendering of Spectra

Rendering Spectra

光谱渲染的几个例子