前言
Matplotlib 的 pcolor 函数能够绘制由一个个四边形(quadrilateral)单元构成的网格数据的彩色图像,相比绘制等值填色图的 contourf 函数,不会产生过度的平滑效果,能忠实反映像元的数值大小,因而在科学可视化中也很常用。本文并不打算介绍该函数的种种,只想着重讨论网格数据的显示效果、shading 参数发挥的作用,以及 pcolor 和 pcolormesh 这对双胞胎间的差异。本文基于 Matplotlib 3.3.4。
图解网格数据
pcolor 全名 pseudo color,即伪彩色。函数签名为
pcolor([X, Y], C, **kw)
其中 X 和 Y 分别是网格的横纵坐标,C 是网格单元内变量的数值。之所以称之为“伪”,是因为 pcolor 并不像 imshow 那样直接用 RGB(A) 数组表示颜色,而是将 C 的数值归一化之后,在一个颜色查找表中查找对应的颜色,进而用颜色差异表现数值大小(原理详见 Matplotlib 系列:colormap 的设置)。C 数组的形状为 (ny, nx),X 和 Y 的形状要比 C 大上一圈,即 (ny + 1, nx + 1),ny 在前表示纵坐标会随数组的行号变动,nx 在后表示横坐标会随数组的列号变动。pcolor 对网格数据的显示效果如下图所示
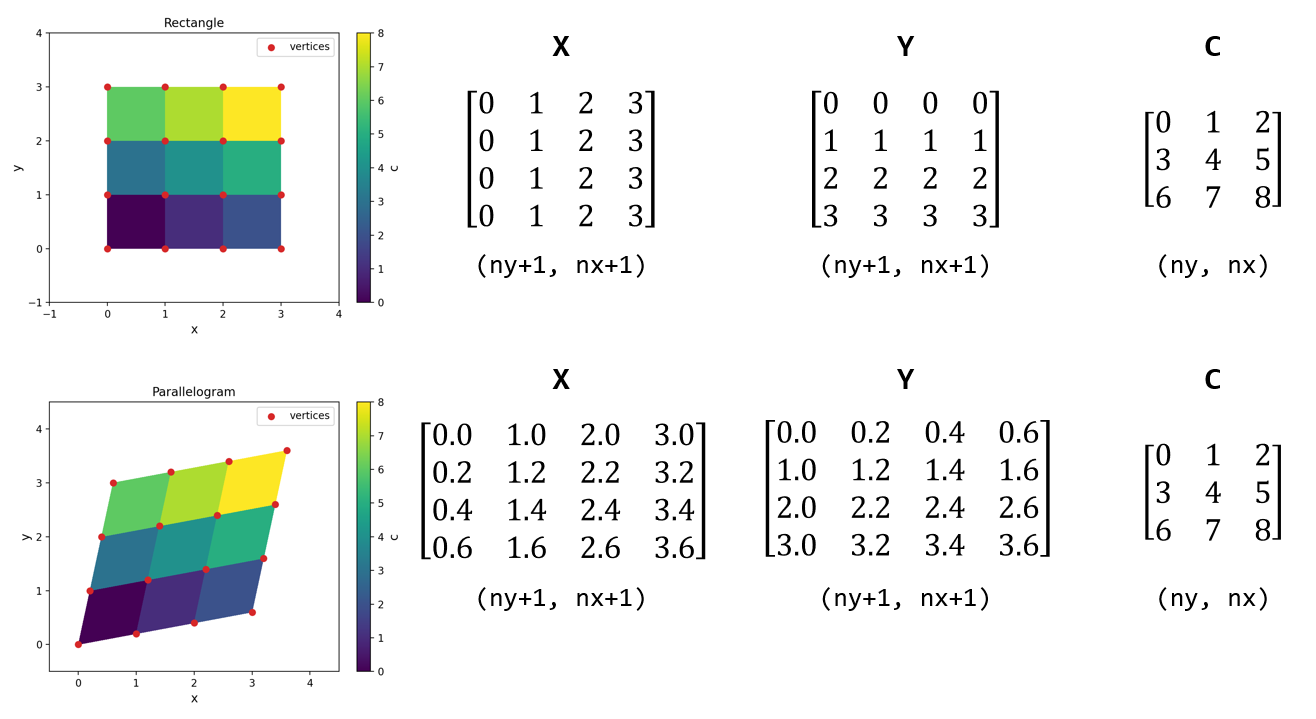
图中第一行是规则网格,即每个网格单元都是矩形(rectangle)。网格顶点用红点表示,X 和 Y 描述了顶点的横纵坐标;四个邻近的顶点围成一个矩形,C 描述了每个矩形内变量的值,pcolor 再根据这些值的大小为矩形涂上相应的颜色——这便是 pcolor 的作用。
显然矩形的边长数总是比间隔数大一,这解释了 X、Y 和 C 在数组形状上的差异。并且正如前面所述,X 的值只会随列号变动,Y 的值只会随行号变动。另外必须注意,数组的起点,即行号和列号都为 0 的元素在数组的左上角,但在画出来的图中这个元素位于左下角,也就是说我们需要区分列号和纵坐标的正方向。
图中第二行是不规则网格,每个网格单元都是平行四边形(parallelogram)。实际上任意四边形都行,因为数组里相邻四个元素的逻辑位置天然构成一个正方形,顶点经由 X 和 Y 的数值可以在 xy 空间映射为任意形状的四边形。注意到,此时 X 和 Y 的值会同时随行号和列号变动,维度 nx 和 ny 不再单纯对应于横坐标和纵坐标。
X 和 Y 还可以是一维数组,此时 pcolor 会利用 X, Y = np.meshgrid(X, Y) 制作对应的规则网格。不给出 X 和 Y 时则会利用从零开始的简单计数制作网格,即
X, Y = np.meshgrid(np.arange(ny + 1), np.arange(nx + 1))
shading 参数
然而世上还有另一种极为常见的网格数据,如下图所示
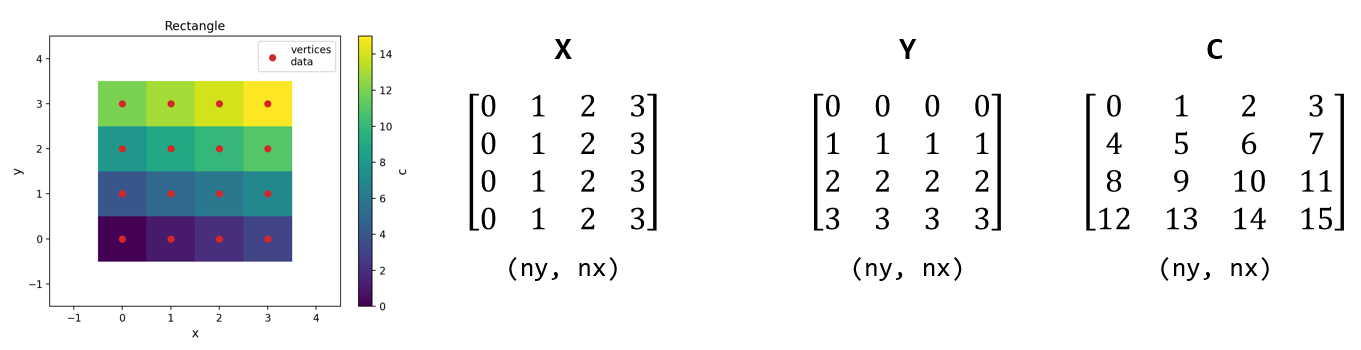
这里 C 的形状与 X 和 Y 完全相同,C 直接描述网格顶点处的变量。气候数值模式输出的格点化产品基本都是这种,例如全球的温压湿风等。由此带来的问题是:原先一个四边形对应一个变量值,相当于四边形中心有一个值;而现在一个四边形的四个顶点都有值,那该选哪个来代表四边形的中心呢?
在 Matplotlib 3.2 及之前的版本里,pcolor 会偷偷抛弃 C 的最后一行和最后一列,即只使用 C[:-1, :-1],从而将数据变成上一节的形式。这样画出来的图不仅会损失一点显示范围,还会因为强行用顶点描述四边形中心,使填色图向对角线方向偏移半个网格单元的长度。
虽然听起来有些可怕,但对画图的实际影响其实不是很大,特别是当网格特别密的时候,少掉一行一列无足轻重,微小的偏移也很难看出来,不过说到底还是不太严谨。新版本的 Matplotlib 给出的解决方案是:推测出一张新的网格,其形状比 C 多出一行一列,并尽可能使每个数据点落在新网格单元的正中心。自 3.3 版本起,可以通过指定参数 shading='nearest' 开启这一功能,而原先丢掉数据的行为称作 'flat'。实现该功能的具体语句是(摘自 _axes.py)
def _interp_grid(X):
# helper for below
if np.shape(X)[1] > 1:
dX = np.diff(X, axis=1)/2.
if not (np.all(dX >= 0) or np.all(dX <= 0)):
_api.warn_external(
f"The input coordinates to {funcname} are "
"interpreted as cell centers, but are not "
"monotonically increasing or decreasing. "
"This may lead to incorrectly calculated cell "
"edges, in which case, please supply "
f"explicit cell edges to {funcname}.")
X = np.hstack((X[:, [0]] - dX[:, [0]],
X[:, :-1] + dX,
X[:, [-1]] + dX[:, [-1]]))
else:
# This is just degenerate, but we can't reliably guess
# a dX if there is just one value.
X = np.hstack((X, X))
return X
X = _interp_grid(X)
Y = _interp_grid(Y)
X = _interp_grid(X.T).T
Y = _interp_grid(Y.T).T
函数 _interp_grid 的功能是:计算数组 X 列与列之间的差分 dX,取 X 的第一列沿列方向偏移 -dX / 2,再取 X 沿列方向偏移 dX / 2,把两个结果并排堆叠成新的 X。旧 X 的形状为 (ny, nx),那么新 X 的形状为 (ny, nx + 1), 同时数值上正好错开差分的一半。反复调用该函数,即可产生在行方向和列方向上都扩展了的新 X 和 Y,形状变为 (ny + 1, nx + 1)。比起仔细研究这个函数,还是看个例子更直观
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib.lines as mlines
def interp_grid(X, Y):
'''插值扩展网格.'''
X = _interp_grid(X)
Y = _interp_grid(Y)
X = _interp_grid(X.T).T
Y = _interp_grid(Y.T).T
return X, Y
def polar_to_xy(r, t):
'''极坐标转xy.'''
x = r * np.cos(np.deg2rad(t))
y = r * np.sin(np.deg2rad(t))
return x, y
# 生成规则网格.
x = np.arange(4)
y = np.arange(4)
X1, Y1 = np.meshgrid(x, y)
# 生成平行四边形网格.
X2 = X1 + 0.2 * Y1
Y2 = 0.2 * X1 + Y1
# 利用极坐标生成不规则网格.
r = np.linspace(2, 4, 5)
t = np.linspace(0, 180, 5)
T, R = np.meshgrid(t, r)
X3, Y3 = polar_to_xy(R, T)
# 收集网格.
data = [(X1, Y1), (X2, Y2), (X3, Y3)]
# 透明cmap.
white = (0, 0, 0, 0)
cmap = mcolors.ListedColormap([white])
# 三个子图对应三组网格.
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
for (X, Y), ax in zip(data, axes):
# 随便生成一个C数组.
C = np.arange(X.size).reshape(X.shape)
# 画出flat的网格.
ax.pcolor(X, Y, C[:-1, :-1], shading='flat', cmap=cmap, ec='k', lw=1)
ax.scatter(X.flat, Y.flat, color='k')
# 画出nearest的网格.
ax.pcolor(X, Y, C, shading='nearest', cmap=cmap, ec='C3', lw=1)
X, Y = interp_grid(X, Y)
ax.scatter(X.flat, Y.flat, color='C3')
# 手动生成图例.
l1 = mlines.Line2D([], [], c='k', lw=1, marker='o', label="'flat'")
l2 = mlines.Line2D([], [], c='C3', lw=1, marker='o', label="'nearest'")
ax.legend(handles=[l1, l2], loc='upper right')
ax.set_xlabel('x', fontsize='large')
axes[0].set_ylabel('y', fontsize='large')
# 调整坐标轴.
axes[0].set_xlim(-1.5, 4.5)
axes[0].set_ylim(-1.5, 4.5)
axes[1].set_xlim(-2, 5)
axes[1].set_ylim(-2, 5)
axes[2].set_xlim(-6, 6)
axes[2].set_ylim(-2, 5)
plt.show()
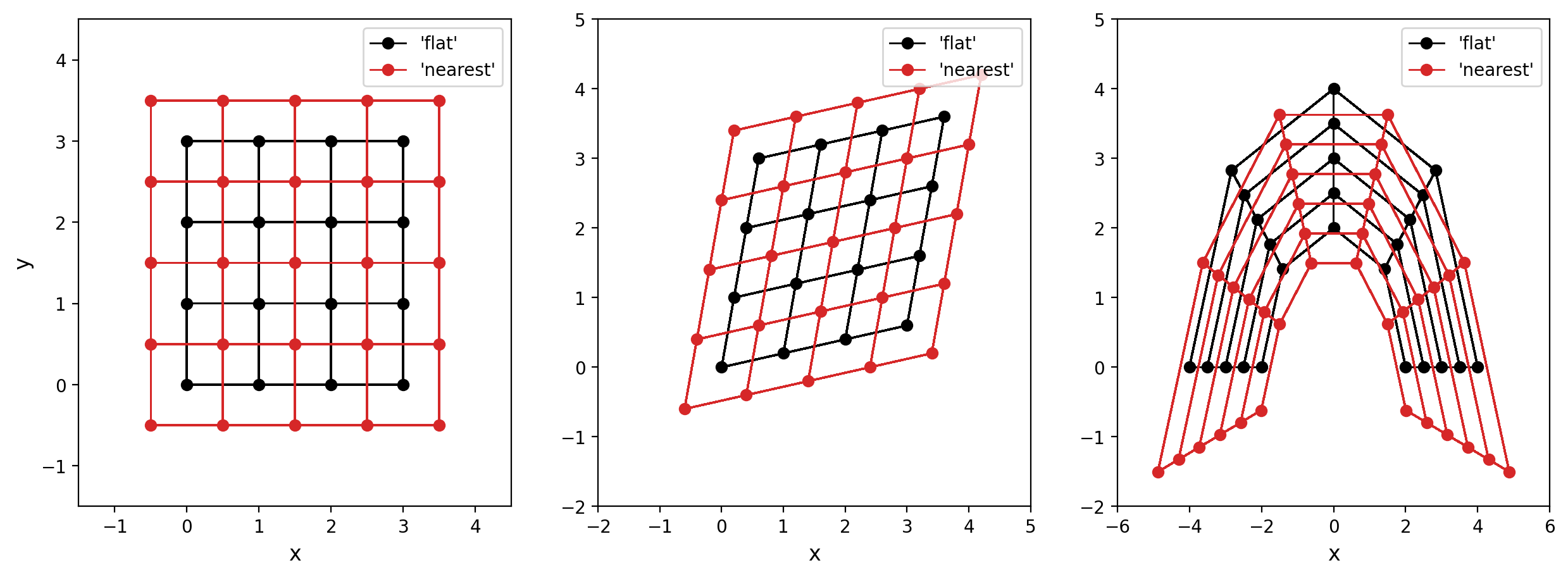
三张图里画的都是当 X、Y 和 C 形状相同时,选取两种 shading 时的网格,区别在于第一张图画的是规则网格,而后两张画的是不规则网格。先说说第一张:
shading='flat':黑点同时是网格顶点和数据点,每个矩形单元的颜色由左下角黑点的值决定。shading='nearest':红色网格根据黑色网格及其间距插值得到,每个黑点正好处在矩形单元的中心,矩形颜色也由这个点的值决定。
这个推测新网格的策略在第一张和第二张图里都表现良好,但在第三张图里,生成的新网格并不能正确包裹数据点,甚至网格形态也有了不小的变化。原因在于,_interp_grid 函数有效的前提是,X 和 Y 在行方向的差分反映的就是纵坐标的差异,在列方向的差分反映的就是横坐标的差异。但上一节已经展示过,对于不规则网格来说,很可能横纵坐标会同时随行或列而变动,所以该函数可能产生预料之外的结果。并且相关代码里也明确表示,这种情况下会弹出 warning 信息警告用户。
除了 'flat' 和 'nearest',还可以指定 shading='gouraud',表示采用计算机图形学中的 Gouraud 着色法,通过线性插值得到平滑的填色效果。不过要求 X、Y 和 C 的形状必须相同,同时只有 pcolormesh 才有这个选项。例如
# 生成规则网格.
x = np.arange(4)
y = np.arange(4)
X, Y = np.meshgrid(x, y)
C = np.arange(X.size).reshape(X.shape)
# 两张子图分别表示两种shading.
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
shadings = ['nearest', 'gouraud']
for shading, ax in zip(shadings, axes):
im = ax.pcolormesh(X, Y, C, shading=shading)
ax.scatter(X.flat, Y.flat, color='C3', label='vertices')
ax.legend(loc='upper right')
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 4)
ax.set_xlabel('x', fontsize='large')
ax.set_title(f"shading='{shading}'", fontsize='large')
axes[0].set_ylabel('y', fontsize='large')
# 设置共用的colorbar.
cbar = fig.colorbar(im, ax=axes)
cbar.set_label('c', fontsize='large')
plt.show()
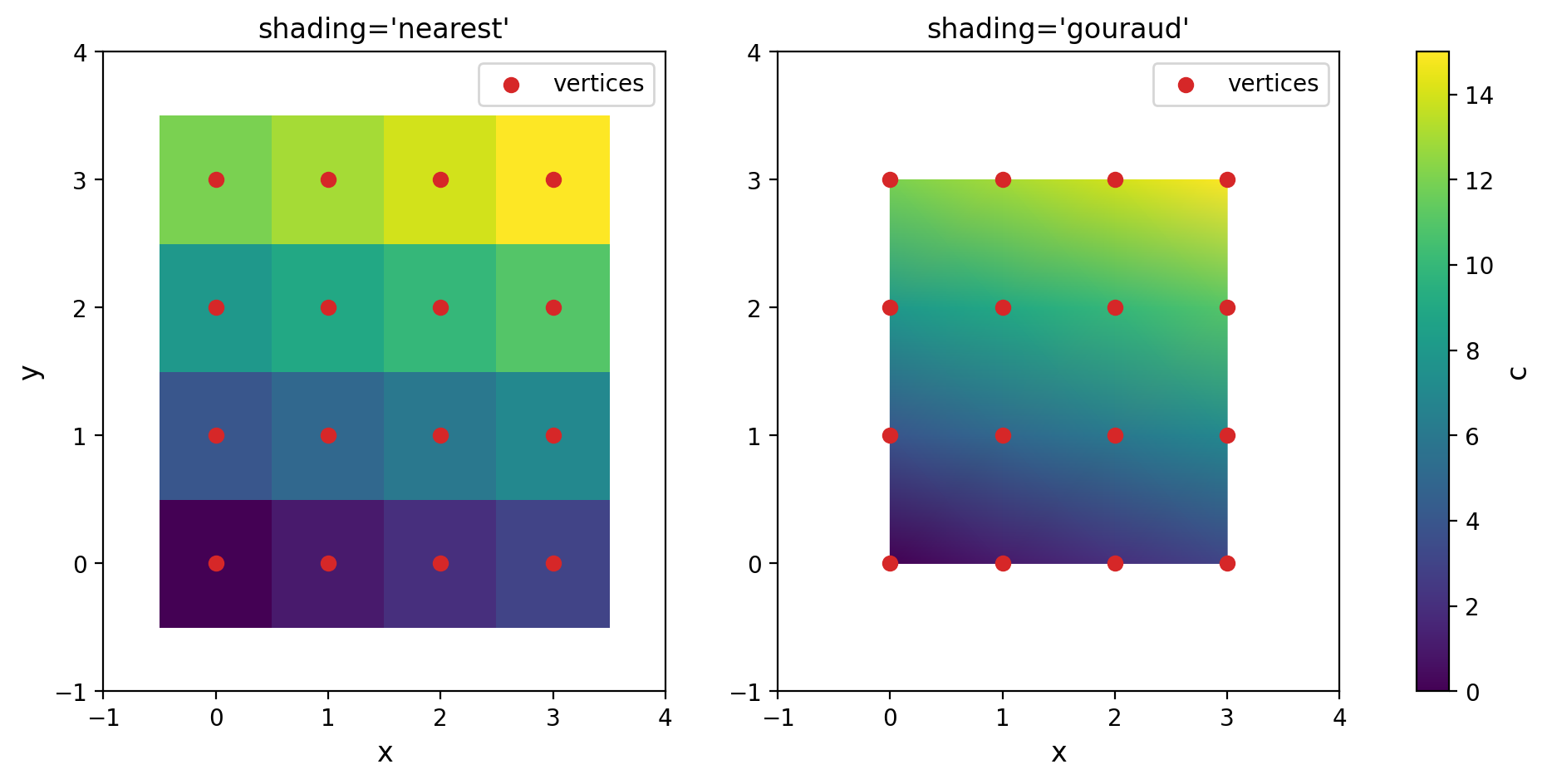
'gouraud' 设置下直接使用原有的网格进行填色,效果甚至比 contourf 还要平滑,当然对于离散的定性数据来说就不要选这个了。
最后梳理一下 shading 参数的使用方法:
-
shading='flat':Matplotlib 3.4 及之前是pcolor的默认参数。当C的形状与X和Y相同时,会自动抛弃最后一行和最后一列(3.3 与 3.4 会产生 warning),而从 3.5 开始会直接报错,要求C的形状必须比X和Y小一圈。 -
shading='nearest':Matplotlib 3.3 开始引入,要求C的形状与X和Y相同。对于不规则网格可能产生错误的效果,建议仅对规则网格使用。 -
shading='auto':Matplotlib 3.3 开始引入,3.5 开始变为pcolor的默认参数。顾名思义会自动根据C的形状决定使用'flat'还是'nearest'。 -
shading='gouraud':pcolormesh独有,要求C的形状与X和Y相同。
pcolor 与 pcolormesh 的差别
Matplotlib 中有两种 pcolor 函数:pcolor 和 pcolormesh。前者返回 PolyCollection 对象,能够记录每个四边形单元的独立结构,因而支持坐标 X 和 Y 含有缺测值;后者返回 QuadMesh 对象,更强调网格整体,画图速度比 pcolor 更快,还专有 'gouraud' 选项,但不允许坐标含有缺测值。由于画图速度的优势,一般推荐使用 pcolormesh。坐标缺测的例子如下
# 创建规则网格.
x = np.arange(5)
y = np.arange(5)
X1, Y1 = np.meshgrid(x, y)
# 复制一份有缺测的网格.
X2, Y2 = X1.astype(float), Y1.astype(float)
X2[2, 2] = np.nan
Y2[2, 2] = np.nan
shape = X1[:-1, :-1].shape
size = shape[0] * shape[1]
C = np.arange(size).reshape(shape)
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
norm = mcolors.Normalize(vmin=C.min(), vmax=C.max())
# 两张子图分别画出pcolormesh和pcolor的结果.
im = axes[0].pcolormesh(X1, Y1, C, shading='flat', ec='k', norm=norm)
im = axes[1].pcolor(X2, Y2, C, shading='flat', ec='k', norm=norm)
cbar = fig.colorbar(im, ax=axes)
cbar.set_label('c', fontsize='large')
# 标出顶点.
axes[0].scatter(X1.flat, Y1.flat, color='k', label='good vertices')
axes[1].scatter(X2.flat, Y2.flat, color='k', label='good vertices')
axes[1].scatter(X1[2, 2], Y1[2, 2], color='m', label='nan vertices')
# 设置坐标等.
for ax in axes:
ax.legend(loc='upper right')
ax.set_xlim(-1, 5)
ax.set_ylim(-1, 5)
ax.set_xlabel('x', fontsize='large')
axes[0].set_ylabel('y', fontsize='large')
axes[0].set_title('pcolormesh', fontsize='large')
axes[1].set_title('pcolor', fontsize='large')
plt.show()
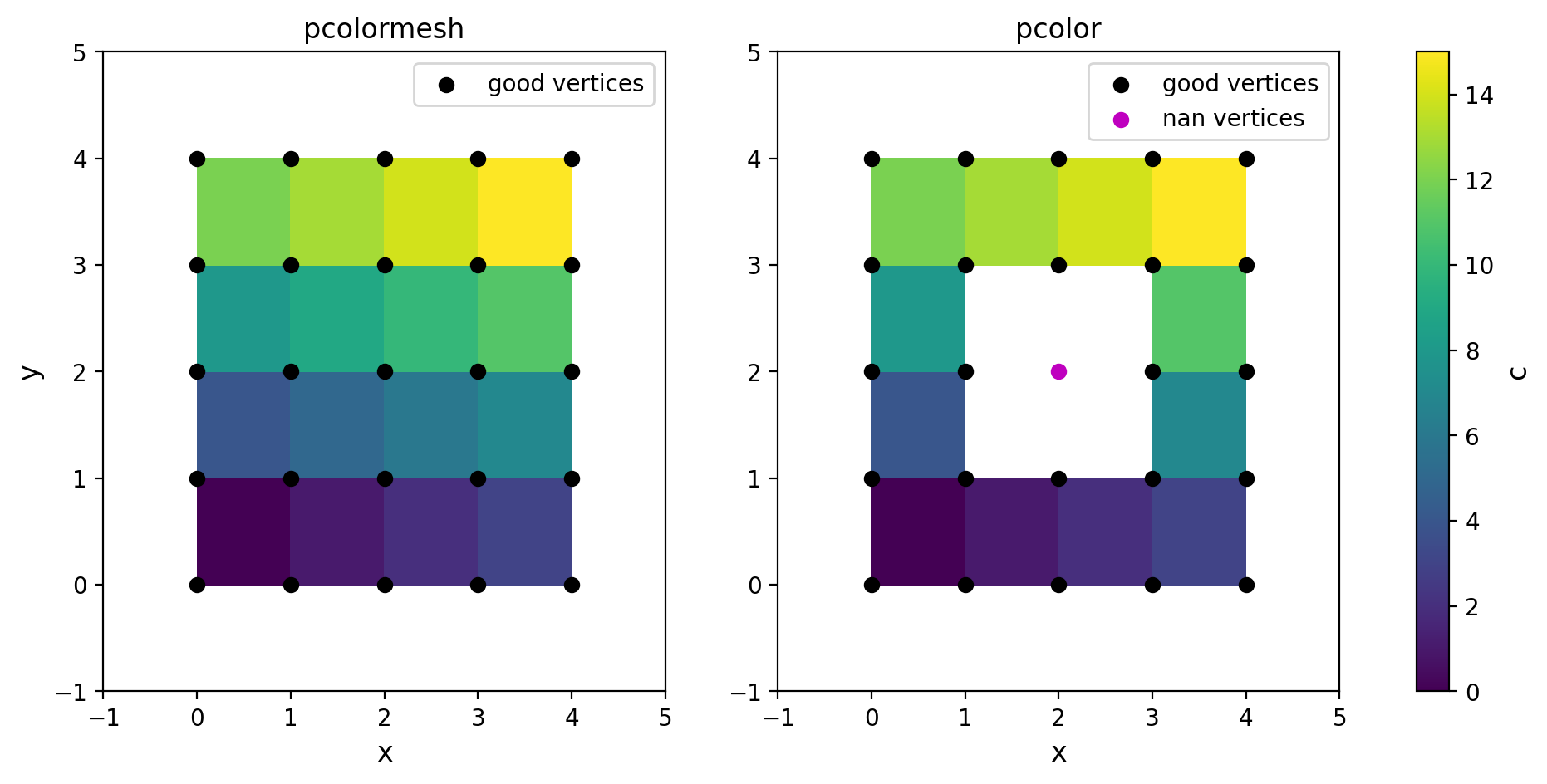
左图和右图绘制的是相同的数据,区别在于左图使用 pcolormesh,右图使用 pcolor 且把网格中心的顶点设为缺测。结果是右图中与紫色顶点相连的四边形全都没画出来,即便这些四边形对应的数据点都是有值的。pcolor 和 pcolormesh 都能正确处理 C 含缺测的情况,默认缺测位置透明,效果可见 NumPy 系列:缺测值处理 的最后一节。
结语
本来 Matplotlib 中的 pcolor 直接效仿了 MATLAB 中 pcolor 的行为,但近期 shading='nearest' 的引入使其有了更丰富的表现力。不过正如前面所展示的,推测新网格的策略对不规则网格效果欠佳,并且是否会影响下游的 Cartopy 地图包的效果也还是个未知数,也许相关的 API 日后还会再变动,烦请多加小心。
参考链接
Make pcolor(mesh) preserve all data