罗切斯特大学朱禺皓的 博客文章,基于颜色匹配实验的原始论文跟后人的调查,先从单位系统和色度系数讲起,再引入颜色匹配函数的概念和计算方法,并直接指出颜色匹配函数就是匹配单位功率单色光的亮度时,红绿蓝三基色的亮度经亮度系数缩放后的值。本文讲解的顺序跟一般教科书相反,显得更加自然和易于理解。专业术语的翻译可能有误,还请读者指正。
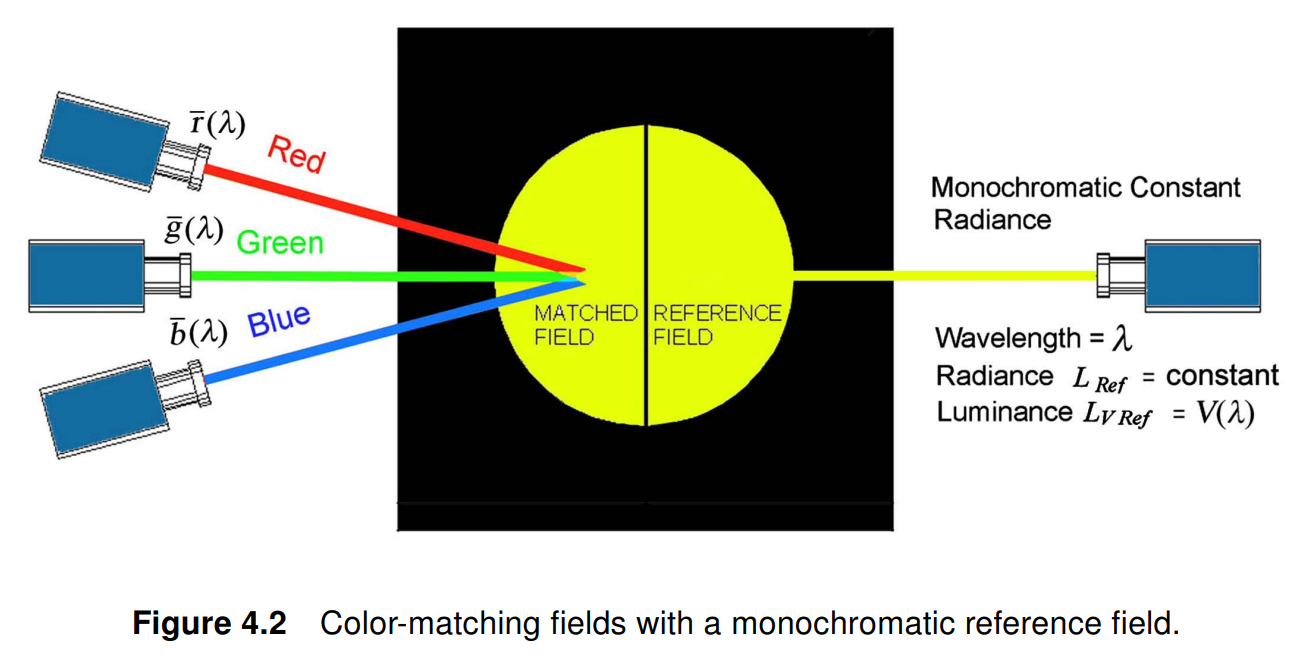
1. 引言
在研究 CIE 1931 RGB 颜色匹配函数(Color Matching Function, CMFs)时,一个常见且合理的疑问是:为什么 CMF 在三基色(primaries)处的值不是 1?例如当 𝛌 = 700 nm 时,即 CIE 1931 RGB 空间中表示红色的基色,R 值为 0.0041(当然 G 和 B 值为 0)。这个 0.0041 表示什么?匹配一个单位的 𝛌 = 700 nm 的红光的颜色正好需要一个单位的 𝛌 = 700 nm 的红光,那对应的 R 值不应该为 1 吗?同样,在 𝛌 = 546.1 nm 和 𝛌 = 435.8 nm 处,即 CIE 1931 标准的绿色基色和蓝色基色,G 和 B 值分别约为 0.215 和 0.2911,显然它们也不为 1。
流行的图形学教科书里都没有解释这一“矛盾”,通常 CMF 的数值只是被称为“权重(weights)”或“数量(amounts)”。比如在第四版的《Real-Time Rendering》中,CMF 被定义为:
The functions relating each set of matching weights to the test patch wavelengths…
第四版的《Fundamentals of Computer Graphics》 里说:
The amount of each (light) required to match a given wavelength λ is encoded in color matching functions…
这些解释还是有点模棱两可。如果 𝛌 = 500 nm 时 RGB 值为 (-0.9494, 1.1727, 0.7767),那么合理的解读是我们需要 -0.9494 个单位的红光,1.1727 个单位的绿光(𝛌 = 546.1 nm),和 0.7767 个单位的蓝光(𝛌 = 435.8 nm),去匹配一个单位的 𝛌 = 500 nm 的单色光的颜色。按这个逻辑,𝛌 = 700 nm 处 CMF 的 R 值就应该是 1。
CIE 1931 的 维基页面 里有这样的注解(不知道谁写的):
Note that rather than specify the brightness of each primary, the curves are normalized to have constant area beneath them.
以及:
The resulting normalized color matching functions are then scaled in the
r : g : bratio of1 : 4.5907 : 0.0601for source luminance and72.0962 : 1.3791 : 1for source radiance to reproduce the true color matching functions.
这些注解非常有用,它们表明 CMF 的数值经历过某种缩放(scaling)和归一化(normalization)操作,因此不能被直接解读。尽管如此,仍存在三个关键问题:
- CMF 的数值到底表示什么?
- CMF 为什么要被归一化?
- CMF 是如何被归一化的?
要回答这些问题,就必须回到最初的颜色匹配实验(距今快一个世纪了),理解原始实验数据如何获取,后续又是如何处理成今天常用的 1931 RGB CMF 的。
这件事困扰了我好些日子,因为原始实验数据相关的信息很不好找。后来我偶然发现了 Arthur Broadbent 的两篇论文2 [Broadbent 2004a, Broadbent 2004b],他详细记录了最初的颜色匹配实验数据在用于构建 CIE 1931 RGB CMF 前所经历的奇妙的变换过程,并在原始数据缺失的地方做了逆向工程。了解这一变换过程不仅能提供历史背景,更重要的是能让我们充分理解 CMF 究竟是什么。
2. 历史
20 世纪 20 年代末,W. D. Wright 和 J. Guild 各做过一次颜色匹配实验。两次实验都是独立进行的,但结果却惊人的一致。Guild 合并了两个实验的数据,并做了一系列数据增强操作(插值和平滑等),由此产生的色度数据构成了 CIE 1931 RGB 空间和 RGB CMF。
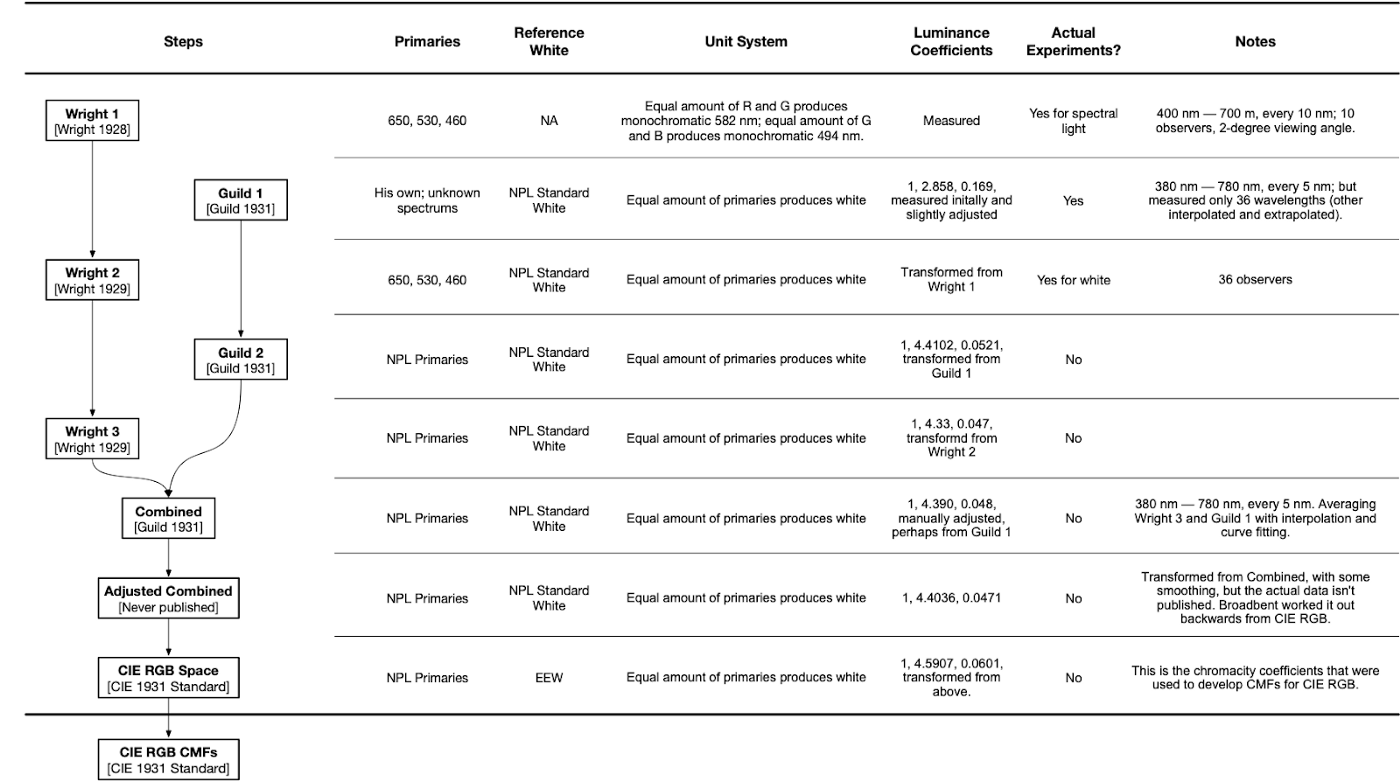
图 1:对最初的 Wright-Guild 颜色匹配实验数据做变换,得出 CIE 1931 RGB CMF 的步骤。
图 1 展示了 Wright 和 Guild 的原始测量数据经变换最终用于构造 1931 CIE RGB CMF 的全过程。之后 RGB 空间数据发展出了 XYZ 空间,论文 [Fairman 1997] 漂亮地总结了 RGB 变换到 XYZ 的详细推导过程。另一篇文章 [Service 2016] 则总结了如何从颜色匹配实验得出 RGB CMF,以及 RGB 空间如何变换到 XYZ 空间,虽然这篇没那么详细,但也包含很多值得一读的见解。
3. 如何量化颜色匹配实验中的光量?
最基本的问题是,一个单位的光到底有多少:是一瓦特、一流明,还是一定量的光子?我们当然可以随意指定一个单位的红光等于含 1 W 能量的红光,或者一个单位的绿光等于含 2 万亿个光子的绿光,又或者一个单位的蓝光等于 43 流明的蓝光。这些单位都是合理的,但对我们来说缺乏有意义的信息。单位的定义应该符合我们的直觉,满足直觉上的要求。没错,单位这一概念非常主观。我们将通过 Wright 和 Guild 实验中的主要步骤来更好地理解这一点。
3.1 Wright 的实验
Wright 在 1928 年的论文 [Wright 1928] 里解释了如何确定单位:
To determine the units of the primaries it is customary to match white by a mixture of the three primaries of the colorimeter in use and to correct the readings as given on the instrument scale by suitable factors, so that for this match all three shall be equal.
关键在于 “for this match all three shall be equal”,即白色应该由等量的三基色产生。这并非客观事实,而只是我们希望拥有的符合直觉的性质:等量的红色、绿色和蓝色产生白色
然后他举例说明:
Suppose that the intensities of the primaries in the colorimeter are controlled by variation of sector openings and that these angular apertures for the white match are 30" for red, 15" for green, and 60" for blue. To correct these readings so that they are in equal proportions, a factor of 2 must be applied to the red and 4 to the green and these factors must be used in any subsequent colour match. Thus, if for a new colour the instrument readings are 40° for red, 10" for green, and 20' for blue, the proportions, in the units agreed upon, are
red 80, green 40, blue 20
giving the trichromatic coefficients as
red 80/140 = .571,green 40/140 = .286,blue 20/140 = .143from which we have the unit equation for the colour as
c = .571R + .286G + .143B
在这个例子中,光的实际功率由光圈(aperture)控制。重要的是,光圈的读数(角度)与放出的光线的实际功率成线性关系,因为放出的光子数量应该线性正比于光圈打开的面积,而这一面积又线性正比于角度3。
为了匹配白光,光圈设置成红光 30°,绿光 15°,蓝光 60°。然后我们决定认为此时红绿蓝是等量的。也就是说,光圈读数为 30° 时放出的红光的数量算一个单位的红光;光圈读数为 15° 时放出的绿光的数量算一个单位的绿光;光圈读数为 60° 时放出的蓝光的数量算一个单位的蓝光。
定义完基色光的单位,我们就能确定匹配任意测试光需要多少数量(即几个单位)的基色光了。在 Wright 的例子里,新颜色 C 的光圈读数为红光 40°,绿光 10°,蓝光 20°,所以我们需要 40/30 个单位的红光,10/15 个单位的绿光,和 20/60 个单位的蓝光来匹配颜色 C4。数量换算为比例即 4 : 2 : 1。
需要注意,此时我们还不知道 C 里有多少光,只知道 40/30 个单位的红光,10/15 个单位的绿光,和 20/60 个单位的蓝光对应一定量的 C 光。
为了量化 C 的数量,Wright 进一步定义:当红绿蓝组分的数量被归一化为加起来等于单位 (1),即 0.571 : 0.286 : 0.143 时,相匹配的 C 光有一个单位的数量。此时红光、绿光和蓝光的相对数量被称为三色系数(trichromatic coefficients),本质上跟现代术语里的色度系数(chromaticity coefficients)是同一个东西。
C = 0.571R + 0.286G + 0.143B
我们有两种方式解读这个方程。首先,一个单位的 C 被定义为 0.571 个单位的红光,0.286 个单位的绿光,和 0.143 个单位的蓝光的混合。其次,一个单位的 C 跟 0.571 个单位的红光,0.286 个单位的绿光,和 0.143 个单位的蓝光的混合光颜色相同。请注意,一个单位红绿蓝所含的光量,对应于真实仪器的读数,而一个单位 C 所含的光量虽然是一种物理属性,但却是从红绿蓝的数量里推导出来的纯概念。
在 Wright 的例子里,通过混合 40/30 个单位的红光,10/15 个单位的绿光,和 20/60 个单位的蓝光,我们得到了 40/30/0.571 = 2.34 个单位的 C。如果我们改变 C 的数量,红绿蓝的数量也会等比例变化,但色度系数保持不变。例如,如果我们想要 2 个单位的 C,应该混合 1.142 个单位的红光,0.572 个单位的绿光,和 0.286 个单位的蓝光,但数量的比例仍为 4 : 2 : 1。
值得注意的是 Wright 在校准基色的单位时并没有指定用于匹配的白光的数量。如果我们将白光的功率加倍,红绿蓝三基色的读数也会加倍成 60°、30° 和 120°。那我们能将 60° 光圈放出的红光的数量定义为一个单位的红光吗?当然可以!同样地,一个单位的绿光(蓝光)就是 30°(120°)光圈放出的绿光(蓝光)的数量。基色光每个单位所含的绝对光量被改变,但它们之间的比例保持不变。因此色度系数也会保持不变。
“单位”的概念涉及光的绝对数量,因为它与光圈的读数直接相关,而光圈读数又控制光的功率。但对于计算色度系数而言,只要单位定义成等量的基色产生白色,那么一个单位所含的光的绝对数量并不重要。因此,无论一个单位的红光是 6 瓦特还是 3 瓦特,都不会改变匹配任意量光线时的色度系数。
总之,计算任意测试光的色度系数的流程为:
- 混合三基色去匹配参考白光,由此定义单位,使得等量的基色能匹配某数量的白光。其中被匹配的白光的绝对数量并不重要。
- 用测试光匹配三基色,记录它们的仪器读数(即光圈孔径角)。同样,测试光的绝对数量不重要。
- 根据第一步中的单位定义,将每种基色的仪器读数转换为该基色的量值。
- 归一化上面的单位数量,使它们的和为 1。这三个归一化后的值即测试光的色度系数。
Wright 以 10 nm 的间隔,对 400 nm 到 700 nm 之间的所有光谱光(spectral lights)做了步骤 2 到 4,得到了这些光的色度系数。他使用的基色光都是单色光:𝛌 = 650 nm 的红光,𝛌 = 530 nm 的绿光,和 𝛌 = 460 nm 的蓝光。参考白光则是英国国家物理实验室(National Physical Laboratory, NPL)的标准白光(具体的功率谱分布见 [Guild 1931] 表 I)。实验中匹配光谱光用到了 10 位观察者,匹配参考白光则用到了 30 位观察者。
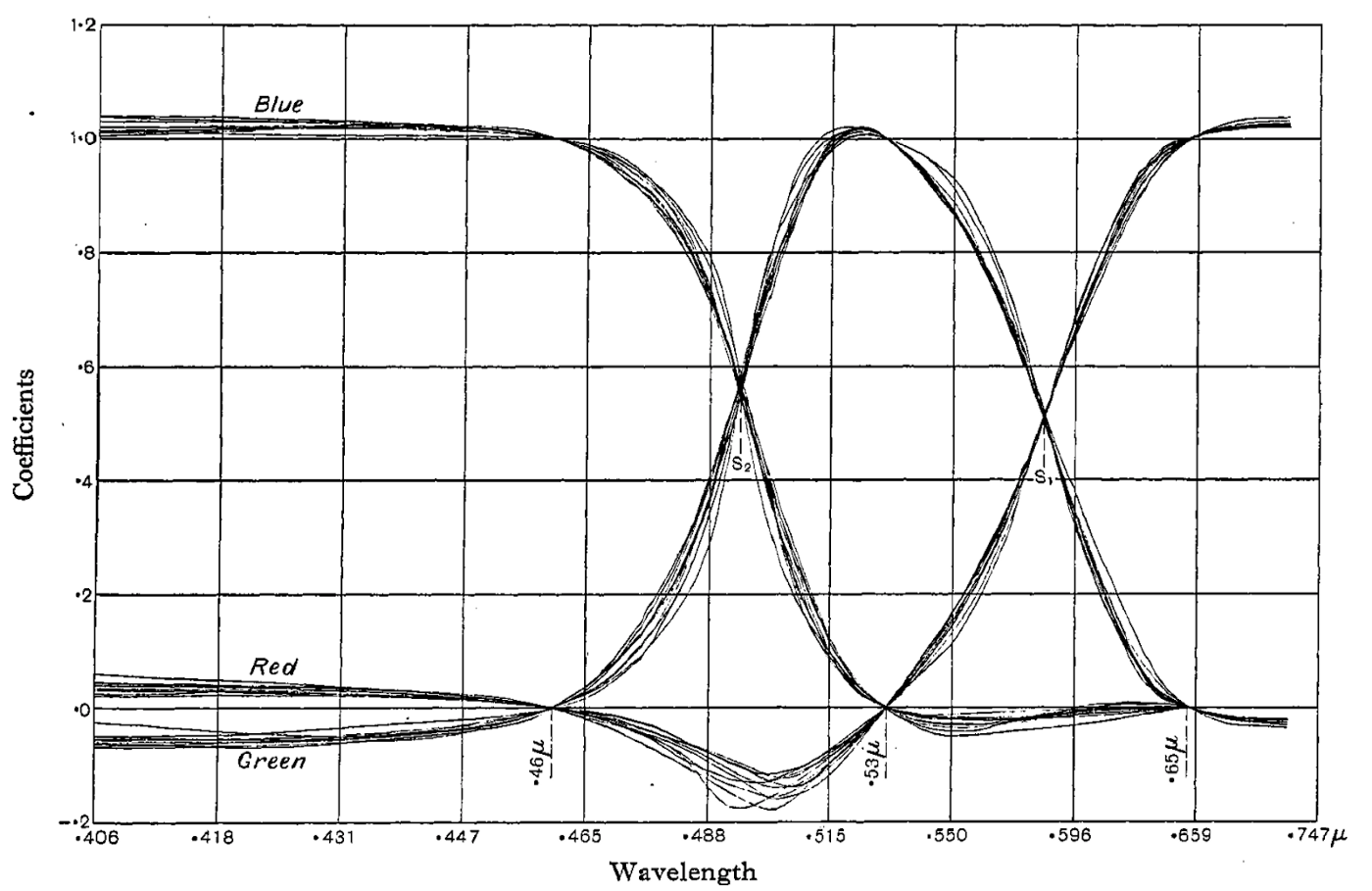
图 2:Wright 初始实验得到的光谱光的色度系数。图自 [Wright 1928]。
摘自 [Wright 1928] 的图 2 展示了所有光谱光的色度系数,其中每条曲线对应一位观察者。
3.2 有益的思想实验:使用反直觉的单位系统
下面做一个有益的思想实验,检查你对概念的理解,并且后续构建 CMF 时也会派上用场:假设我们的直觉变成 1 : 2 : 3 的基色产生白色,而非 1 : 1 : 1。这个比例无所谓对错,但会改变一个单位的光含有的绝对数量,同时色度系数也会跟着改变。
我们可以进行如下的推理。假设在旧的单位系统里,一定量的白光由各一个单位的基色构成;而现在同样数量的白光在新的单位系统里,将由 k 个单位的红光,2k 个单位的绿光,和 3k 个单位的蓝光构成。其中 k 是一个缩放因子(scaling factor),具体值不清楚,因为我们只需要知道产生白光的基色的比例,而不需要知道确切的数量。因此得到下面的方程:
R + G + B = k R' + 2k G' + 3k B'
其中 R、G、B 代表旧单位系统里一个单位的红光、绿光、蓝光;而 R'、G'、B' 代表新单位系统里一个单位的红光、绿光、蓝光。方程里用两种不同的方式表示了相同数量的白光,这意味着:
- 旧系统里一个单位的红光等价于新系统里 k 个单位的红光
- 旧系统里一个单位的绿光等价于新系统里 2k 个单位的红光
- 旧系统里一个单位的蓝光等价于新系统里 3k 个单位的红光
用于测试的 C 光在旧系统里表示为:
C = 0.571 R + 0.286 G + 0.143 B
它在新系统里表示为:
C = 0.571k R' + 0.286(2k) G' + 0.143(3k) B'
对系数做归一化使它们的和为 1,由此得到一个单位的 C 在新单位系统里的定义:
C = 0.571k/(0.571k + 0.286(2k) + 0.143(3k)) R' +
0.286(2k)/(0.571k + 0.286(2k) + 0.143(3k)) G' +
0.143(3k)/(0.571k + 0.286(2k) + 0.143(3k)) B'
消去 k 得到:
C = 0.571/(0.571 + 0.286×2 + 0.143×3) R' +
0.286×2/(0.571 + 0.286×2 + 0.143×3) G' +
0.143×3/(0.571 + 0.286×2 + 0.143×3) B'
= 0.363 R' + 0.364 G' + 0.273 B'
(0.363, 0.364, 0.273) 便是 C 在新单位系统里的色度系数。
可以观察到两个关键的点:首先,仅仅因为我们改变了单位的定义方式,新系数的值就不同于原始系数 (0.571、0.286、0.143) 了。有三个重要因素决定了色度系数:(1) 基色的选择;(2) 参考白光的选择;(3) 我们用来定义单位的“直觉”。
其次,新的色度系数可以从原始色度系数中推导出来,不依赖于 k 的具体值。
一个很实际的问题是,Wright 的初始数据基于他自己挑选的基色(𝛌 = 650 nm 的红光,𝛌 = 530 nm 的绿光,𝛌 = 460 nm 的蓝光)。然而当时 NPL 使用的标准基色与此不同,为 𝛌 = 700 nm 的红光,𝛌 = 546.1 nm 的绿光,𝛌 = 435.8 nm 的蓝光。因此为了与他人的数据进行比较和匹配,他需要用某种方式将自己的数据变换成基于 NPL 标准基色的数据。当然他可以改用 NPL 标准基色重做所有实验,但这也许只是浪费时间。聪明的 Wright 提出了一种巧妙的方法,在原始数据的基础上“合成(synthesizing)”结果,让实验看起来就像是基于 NPL 标准基色做的一样。[Wright 1929] 里描述了这一方法,[Broadbent 2004] 对此也有很好的总结。
3.3 Guild 的实验
与此同时 Guild 用 7 位观察者做了类似的实验(实际上比 Wright 还早一年),基于他自己挑选的三基色光,以 NPL 标准白光作为参考白光。不出所料,定义单位时也要求等量的基色组合起来可以匹配 NPL 标准白光。
Guild 并没有记录基色具体的光谱,只是简单提到,基色是通过“让乳白灯泡的白炽灯发出的光线穿过红绿蓝明胶滤光片”得到的。他在该实验中以 5 nm 的间隔得到了 380 nm 到 700 nm 间所有光谱光的色度系数。
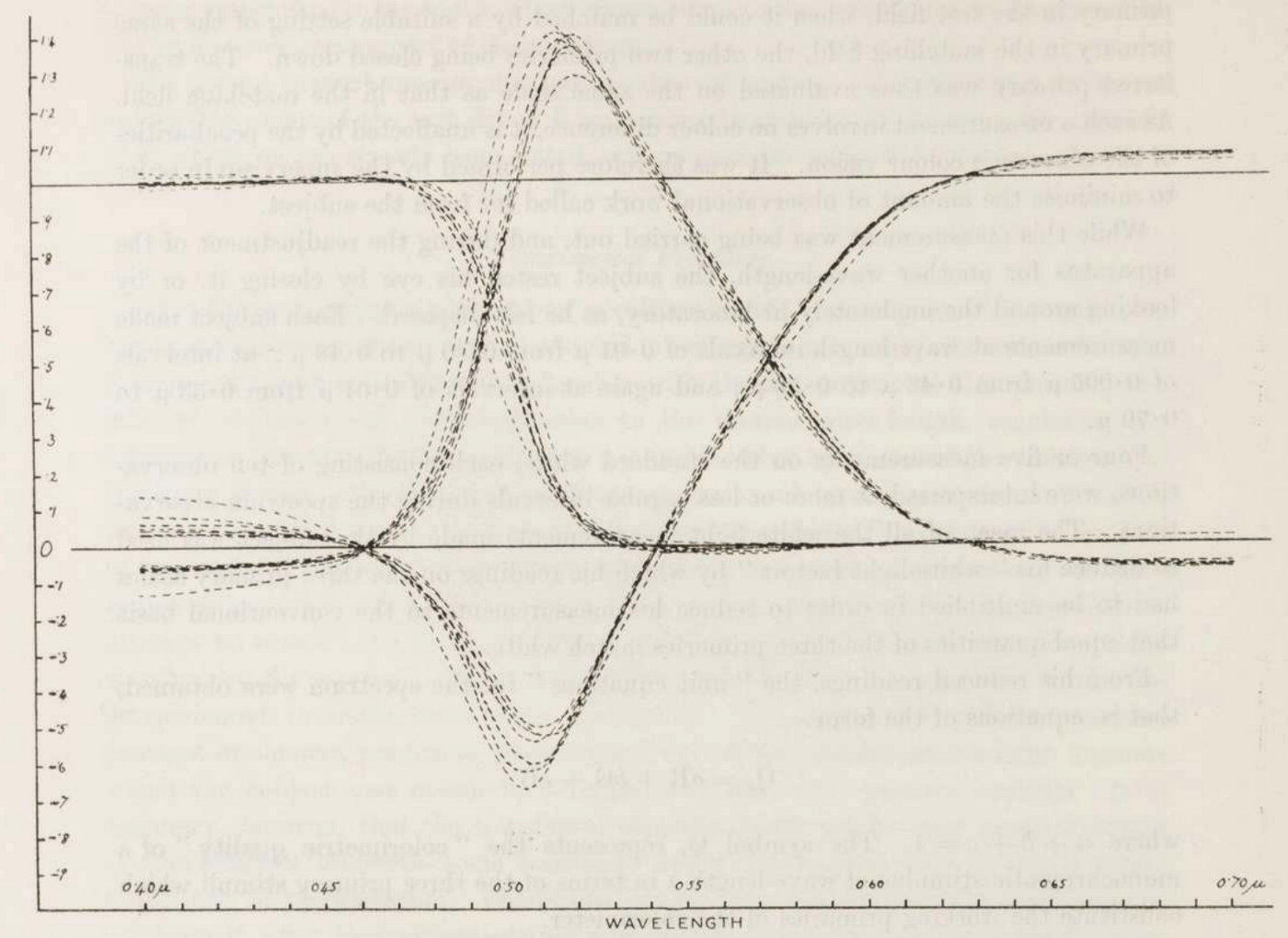
图 3:Guild 初始实验中光谱光的色度系数。图自 [Guild 1930]。
图 3 取自 [Guild 1930],展示了测量出的光谱色度系数,其中每条曲线对应一位观察者。你可能已经注意到了,虽然图 2 和图 3 都绘制了色度系数,但它们略有不同。原因在于使用的基色、参考白光和单位系统不同。图 2 对应图 1 中的“Wright 1”步骤,而图 3 对应图 1 中的“Guild 1”步骤。两张图之间的对比清楚显示了基色、参考白光和单位系统的重要性。
与 Wright 类似,Guild 随后“合成”了他的数据,就好像实验是基于 NPL 基色做的一样,同时仍以 NPL 标准白光作为参考白光。
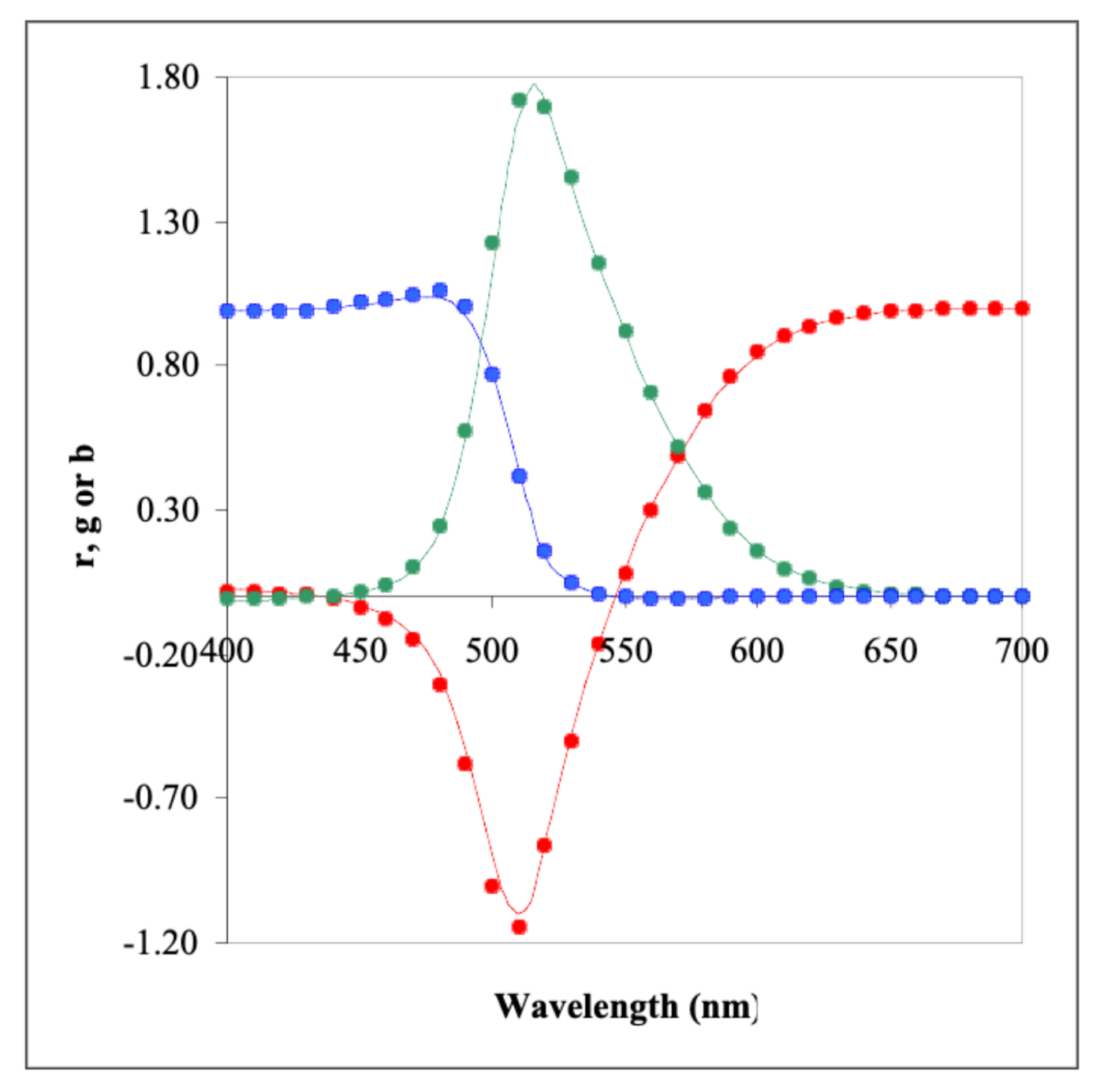
图 4:Wright 和 Guild 得到的色度系数的对比。图自 [Broadbent 2004b]。
此时 Guild 和 Wright 的数据都处于完全相同的系统里(基色 + 参考白光 + 单位系统),所以可以进行比较。当 Guild 合并两组数据时,它们非常吻合。摘自 [Broadbent 2004b] 的图 4 比较了这两组数据,其中点表示 Wright 的数据,线表示 Guild 的数据。三种颜色对应三基色的光谱色度系数。
考虑到两组数据是独立测出的,使用完全不同的基色、观察者和实验设置,图中近乎完美的匹配令人称奇。此外 Guild 用来比较的两组数据甚至不是原始实验数据,而是经合成/变换后的数据。这种几乎完美的一致性使人们有信心为色彩空间定义出一套标准。
Guild 又陆续对数据做了增强处理(平均、曲线拟合、平滑等),以使他的数据与 Wright 的数据相统一,由此得出了最终的光谱色度系数。我们通常用 r(𝛌)、g(𝛌) 和 b(𝛌) 表示波长为 𝛌 的光谱光的色度系数。
4. 亮度系数:改变参考白光
在利用数据导出 CMF 前还有最后一步。CIE 1931 标准里的参考白光不是 NPL 标准白光,而是一种假想的等能量白光(EEW),在所有波长上具有相同的能量或功率。Guild 利用手中的数据合成了基于 EEW 的光谱色度系数,就好像他们真的用 EEW 作为参考白光做了实验一样。
为了理解 Guild 的变换操作,我们需要知道一个关键的新概念:亮度系数(luminance coeffcient)。Guild 和 Wright 在他们的论文里称其为相对亮度(relative luminance)或亮度因子(luminosity factor)。接下来介绍变换的原理。
问题设置如下。已知波长为 𝛌 的光谱光基于 NPL 标准基色,以 NPL 标准白光为参考白光时的色度系数,需要计算以 EEW 为参考白光时该光新的色度系数(仍使用 NPL 标准基色)。
Guild 的方法是弄清楚旧系统中需要多少个单位的基色才能匹配 EEW。如果我们能计算出这些数值,就能将问题转化为之前的思想实验。为了得到基色的比例,我们将逐个波长地进行计算。基本思路是,对构成 EEW 的每个波长的光,明确旧系统中需要多少单位的基色来匹配该光的亮度(luminance)。然后将它们相加以得到基色总的量值,再标准化为 1 得出实际比值。
为了不失一般性,假设 EEW 光谱上每个波长的功率都为 P。EEW 在 𝛌 波长处的单色组分用 NPL 标准基色在旧单位系统(即参考白光为 NPL 标准白光)中表示为:
W(𝛌) = M(𝛌)(r(𝛌)R + g(𝛌)G + b(𝛌)B)
其中 R、G、B 分别是旧系统中一个单位的红光、绿光、蓝光,r(𝛌)、g(𝛌)、b(𝛌) 是旧系统中波长 𝛌 的色度系数,而 M(𝛌) 是未知的缩放因子,使得 M(𝛌)r(𝛌)、M(𝛌)g(𝛌)、M(𝛌)b(𝛌) 分别表示匹配 𝛌 处的 EEW 所需的红绿蓝的绝对数量(以单位计)。注意 M(𝛌) 会随 𝛌 的变化而变化。
在 EEW 的全光谱上对 𝛌 进行积分,得到匹配 EEW 所需的红绿蓝的总量(以单位计):
r = ∑M(𝛌)r(𝛌)
g = ∑M(𝛌)g(𝛌)
b = ∑M(𝛌)b(𝛌)
因此 EEW 可以表示为
EEW = rG + gG + bB
那怎么得到 M(𝛌) 呢?关键在于利用亮度的不变性:EEW 在任意波长 𝛌 处的亮度应该等于匹配该波长的基色光的总亮度。毕竟这也是我们生成任意复杂光谱对应颜色的方法。
计算 EEW 在特定波长 𝛌 处的亮度很简单:等于 P * V(𝛌),其中 V(𝛌) 是亮度效率函数(luminance efficiency function),Guild 也称其为日视功效函数(photopic efficacy function),由 CIE 在 1924 年测量得到。这里我们忽略常数因子(683 lm/W)。
但波长 𝛌 处三基色的亮度怎么计算呢?已知波长 𝛌 所需三基色的绝对数量(即 M(𝛌)r(𝛌)、M(𝛌)g(𝛌) 和 M(𝛌)b(𝛌) ),但怎么把光的数量和亮度联系起来?色度系数只是比例,不含亮度相关的信息,只表示为了创造任意数量的单色光 𝛌 的颜色,三基色量值的比例应该为 r(𝛌) : g(𝛌) : b(𝛌)。无论单色光的数量是多少,比值都保持不变。想匹配数量更多的 𝛌 光就需要更多基色光,反之亦然。显然我们还缺少一些蕴含亮度信息的东西。
为此需要引入亮度系数的概念。在特定系统中,光的亮度系数定义为一个单位的光的亮度。通常还要对三基色的亮度系数进行缩放,使红光的系数为 1。在 Guild 的实验里,他测量并计算出了 NPL 标准基色的亮度系数,Lʳ、Lᵍ 和 Lᵇ,如下所示5:
Lʳ = 1.0000
Lᵍ = 4.4036
Lᵇ = 0.0471
𝛌 处红绿蓝的总亮度即:
M(𝛌)r(𝛌)LʳN + M(𝛌)g(𝛌)LᵍN + M(𝛌)b(𝛌)LᵇN
其中 N 是未知的缩放因子。于是有:
V(𝛌)P = M(𝛌)r(𝛌)LʳN + M(𝛌)g(𝛌)LᵍN + M(𝛌)b(𝛌)LᵇN
因此可以计算 M(𝛌):
M(𝛌) = V(𝛌)P / N(r(𝛌)Lʳ + g(𝛌)Lᵍ + b(𝛌)Lᵇ)
其中 V(𝛌)、r(𝛌)、g(𝛌)、b(𝛌)、Lʳ、Lᵍ、Lᵇ 的值都是已知的,P/N 是未知的缩放因子。不妨令:
U(𝛌) = V(𝛌) / (r(𝛌)Lʳ + g(𝛌)Lᵍ + b(𝛌)Lᵇ)
以及 P/N = C,得到:
M(𝛌) = U(𝛌)C
于是,
r = ∑M(𝛌)r(𝛌) = C∑U(𝛌)r(𝛌),
g = ∑M(𝛌)g(𝛌) = C∑U(𝛌)g(𝛌),
b = ∑M(𝛌)b(𝛌) = C∑U(𝛌)b(𝛌).
这意味着 EEW 在旧单位系统里表示为:
EEW = C∑U(𝛌)r(𝛌) R + C∑U(𝛌)g(𝛌) G + C∑U(𝛌)b(𝛌) B
因此,EEW 在旧单位系统里的色度系数为:
Wr = ∑U(𝛌)r(𝛌) / (∑U(𝛌)r(𝛌) + ∑U(𝛌)g(𝛌) + ∑U(𝛌)b(𝛌))
Wg = ∑U(𝛌)g(𝛌) / (∑U(𝛌)r(𝛌) + ∑U(𝛌)g(𝛌) + ∑U(𝛌)b(𝛌))
Wb = ∑U(𝛌)b(𝛌) / (∑U(𝛌)r(𝛌) + ∑U(𝛌)g(𝛌) + ∑U(𝛌)b(𝛌))
可见未知缩放因子 C(即 P/N)消去了。Guild 计算出 Wr、Wg 和 Wb 的值为 0.3013、0.3140 和 0.38476。
这个结果非常重要,因为现在我们知道了旧单位系统中 EEW 是由 Wr : Wg : wb 比例的红绿蓝混合得到的。另外根据定义,新单位系统中 EEW 应该以 1 : 1 : 1 的比例混合。于是问题本质上变回了我们之前做过的思想实验!使用跟前面相同的方法,就能将任意光谱光的色度系数从旧单位系统(以 NPL 标准白光为参考白光)转换到新单位系统(以 EEW 为参考白光)。
最后一点,新单位系统中的亮度系数也必须改变。亮度系数表示一个单位的光的相对亮度,因为新系统里一个单位的意义被改变,所以亮度系数也肯定要跟着修改。那这该怎么计算呢?新系统里一个单位的红光等价于旧系统里 Wr 个单位的红光,后者的总亮度为 WrLʳ,在新系统里变成了一个单位红光的亮度。同样的过程也适用于绿光和蓝光。按红光系数为 1 的方式将新系统里的亮度归一化,得到的新亮度系数的值如下所示,后续将用来构造 CMF:
Lʳ = 1.0000
Lᵍ = 4.5907
Lᵇ = 0.0601
总结一下,本节按 CIE 1931 标准的设置,以 NPL 基色作为基色光,EEW 作为参考白光,定义等量基色光产生一定量参考白光的单位系统,计算出了所有光谱光的色度系数。
图 5 绘制了用于 CIE 1931 RGB 空间的光谱色度系数。可以看到 R 值在 𝛌 = 700 nm 确实为 1,𝛌 = 546.1 nm 处 G 值为 1,𝛌 = 435.8 nm 处 B 值为 1,与我们的直觉相符。不过这些曲线还不能算是颜色匹配函数!
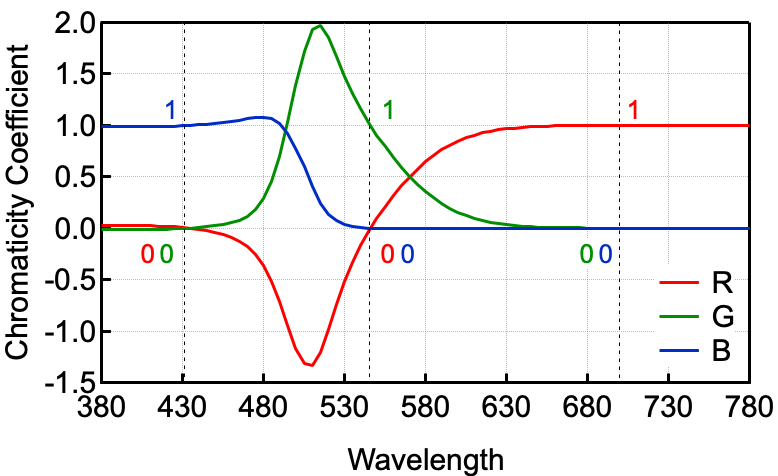
图 5:CIE 1931 RGB 空间里的光谱色度系数。
需要注意,亮度系数和 V(𝛌) 存在一个很关键的区别:V(𝛌) 表示单位功率的相对亮度,而亮度系数表示单位光量的相对亮度。一个单位的功率和一个单位的光是不同的——前者量化了一个绝对物理量,而后者是相对于我们使用的单位系统而言的。1 个单位的 R 可以有 100 瓦特,1 个单位的 B 可以有 5 瓦特,或者其它值都可以。
5. 从色度系数到 CMF
现在我们终于有了用来导出 CMF 的数据。本节先解释 CMF 的用途,然后解释如何从色度函数(chromaticity function)构造 CMF,好让 CMF 按预期派上用场。
5.1 为什么需要 CMF?
我们的目标是:通过混合三种基色光产生所有颜色,无论颜色的功率谱分布(Spectral Power Distribution, SPD)有多复杂。也就是说,对于给定的 SPD,我们想知道需要多少单位的基色来匹配其颜色。而计算基色的总量需要“逐步进行”:先计算匹配单色光 𝛌 所需的基色的量,然后将所有波长所需的基色数量相加,计算出匹配目标光的基色总量。不过仅有色度图还不够,因为 SPD 表示功率的绝对数值,而色度仅表示比例关系。
不妨令目标光 T 的 SPD 为 𝚽,其在波长 𝛌 处的功率为 𝚽(𝛌)。问题是如何确定匹配单色光 𝛌 需要多少单位的基色?色度系数 r(𝛌)、g(𝛌) 和 b(𝛌) 只告诉我们应该以什么比例混合基色来产生一个单位的单色光 𝛌,但我们想确定具体需要混合多少基色来匹配 𝚽(𝛌) 瓦特的单色光 𝛌。
CMF 就是为了解决这一问题而引入的。颜色匹配函数 R()、G()、B() 定义为匹配 𝚽 上每种单色光 𝛌 的单位功率亮度所需的红光、绿光、蓝光的数量(以单位计)。因此获取 CMF 后就能计算目标光 T 在 𝛌 处所需的基色的量。下面是详细步骤。
目标光 T 在 𝛌 处的功率为 𝚽(𝛌)。因为匹配一瓦特的单色光 𝛌 的亮度需要 R(𝛌) 个单位的红光、G(𝛌) 个单位的绿光,和 B(𝛌) 个单位的蓝光,所以匹配目标光中单色光 𝛌 的亮度自然需要 𝚽(𝛌)R(𝛌) 个单位的红光、𝚽(𝛌)G(𝛌) 个单位的绿光,和 𝚽(𝛌)B(𝛌) 个单位的蓝光。
因此为了匹配目标光的每一部分,需要 ∑𝚽(𝛌)R(𝛌) 个单位的红光、∑𝚽(𝛌)G(𝛌) 个单位的绿光,和 ∑𝚽(𝛌)B(𝛌) 个单位的蓝光。如果 SPD 是连续的而非离散样本,那么得到下列熟悉的方程:
Rt = ∫𝚽(𝛌)R(𝛌)d𝛌
Gt = ∫𝚽(𝛌)G(𝛌)d𝛌
Bt = ∫𝚽(𝛌)B(𝛌)d𝛌
匹配 SPD 为 𝚽 的目标光所需的红光、绿光和蓝光的绝对数量即 Rt、Gt 和 Bt。同时 Rt、Gt 和 Bt 间的比值就是目标光的色度系数,即产生一个单位的 T 所需的红绿蓝的量。Rt、Gt 和 Bt 的现代术语是 T 的三刺激值(tristimulus values)。
5.2 如何构造 CMF
我们已经知道了怎么用 CMF 生成颜色,下一个问题是如何构造 CMF 呢?
请记住,色度系数 r(𝛌)、g(𝛌) 和 b(𝛌) 表示应该以什么比例混合基色以获取一个单位的单色光 𝛌。现在假设为了匹配功率为一个单位的单色光 𝛌 的亮度,需要 k(𝛌)r(𝛌)、k(𝛌)g(𝛌) 和 k(𝛌)b(𝛌) 个单位的基色。为了维持单色光 𝛌 的色度,这里基色数量的比例为 r(𝛌) : g(𝛌) : b(𝛌)。
单色光 𝛌 的单位功率亮度为 V(𝛌),而三基色在 𝛌 处的总亮度为 Lʳk(𝛌)r(𝛌) + Lᵍk(𝛌)g(𝛌) + Lᵇk(𝛌)b(𝛌),因此有 V(𝛌) = Lʳk(𝛌)r(𝛌) + Lᵍk(𝛌)g(𝛌) + Lᵇk(𝛌)b(𝛌)。
于是可以计算 k(𝛌):
k(𝛌) = V(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌))
分母 Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌) 可以视作单色光 𝛌 的亮度系数,这也是线性系统假设应用于亮度系数的一个例子。
有了 k(𝛌) 就能计算三个 CMF 了:
R(𝛌) = k(𝛌)r(𝛌) = V(𝛌)r(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌))
G(𝛌) = k(𝛌)g(𝛌) = V(𝛌)g(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌))
B(𝛌) = k(𝛌)b(𝛌) = V(𝛌)b(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌))
译注:按前文思想实验里的步骤,k(𝛌)r(𝛌) 乘上未知因子 N 才表示亮度。那这里是漏掉 N 了吗?译者的理解是,这里所求的 CMF,实际上是一种乘以亮度系数后直接等于亮度的数量。
因此 CMF 可以理解为 r(𝛌)、g(𝛌) 和 b(𝛌) 缩放后的结果。注意 k(𝛌) 不是常数,是关于 𝛌 的函数。下图为 CIE 1931 RGB 的 CMF:
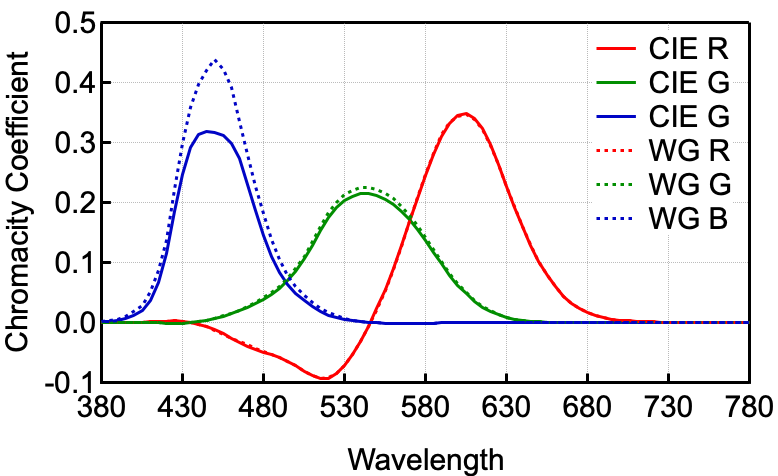
图6:CIE CMF(实线)和 Wright-Guild 数据得出的 CMF(虚线),前者的参考白光是 EEW,后者是 NPL 标准白光。
CMF 的一个重要性质是它的值跟基色和参考白光的选取都有关系,但参考白光有影响的事实经常被忽视!这是因为参考白光决定了“一个单位”对于基色的意义,由此影响到 r(𝛌)、g(𝛌)、b(𝛌)、Lʳ、Lᵍ 和 Lᵇ。
图 6 展示了 CIE 1931 RGB CMF(实线),作为对比还叠加了基于合并的 Wright-Guild 数据的 CMF(虚线)。前者的参考白光是 EEW,后者是 NPL 标准白光。可以看到这两个系统的 CMF 趋势一致,但仍存在不同。这说明 CMF 确实取决于参考白光的选取。
5.3 CIE 1931 RGB CMF 的性质
1. EEW 的 RGB 三刺激值都相等,因为单位系统的定义里就要求 EEW 由等量基色混合而得。因此,
∫𝚽(𝛌)R(𝛌)d𝛌 = ∫𝚽(𝛌)G(𝛌)d𝛌 = ∫𝚽(𝛌)B(𝛌)d𝛌
因为 EEW 所有波长的 𝚽(𝛌) 都为 1(常数),所以有:
∫R(𝛌)d𝛌 = ∫G(𝛌)d𝛌 = ∫B(𝛌)d𝛌
这三个积分表示 CMF 曲线下面的面积,这就是为什么开头引用的维基百科里说:
Note that rather than specify the brightness of each primary, the curves are normalized to have constant area beneath them.
2. 根据定义,任意波长 𝛌 都满足 V(𝛌) = LʳR(𝛌) + LᵍG(𝛌) + LᵇB(𝛌)。方程两边均表示 1 W 的单色光 𝛌 具有的亮度。
对两边积分得:
∫V(𝛌)d𝛌 = ∫LʳR(𝛌)d𝛌 + ∫LᵍG(𝛌)d𝛌 + ∫LᵇB(𝛌)d𝛌
= Lʳ∫R(𝛌)d𝛌 + Lᵍ∫G(𝛌)d𝛌 + Lᵇ∫B(𝛌)d𝛌
因为 ∫R(𝛌)d𝛌 = ∫G(𝛌)d𝛌 = ∫B(𝛌)d𝛌,所以:
∫R(𝛌)d𝛌 = ∫G(𝛌)d𝛌 = ∫B(𝛌)d𝛌 = ∫V(𝛌)d𝛌 / (Lʳ + Lᵍ + Lᵇ)
三条 CMF 曲线下的面积不仅相等,且等于 V(𝛌) 曲线面积的 1 / (Lʳ + Lᵍ + Lᵇ) 倍。
3. 如今 CIE 1931 RGB 空间的光谱色度系数是由 CMF R(𝛌)、G(𝛌) 和 B(𝛌) 计算而来的。但正如我们所见,当年 Guild 和 Wright 是先计算光谱色度系数 r(𝛌)、g(𝛌) 和 b(𝛌) 再导出 CMF。那么这两种计算方式的不同会改变光谱色度系数的数值吗?
答案是不会。因为从前面的方程可以看到,R(𝛌) : G(𝛌) : B(𝛌) 跟 r(𝛌) : g(𝛌) : b(𝛌) 是相同的。CMF 只不过是色度系数乘以 k(𝛌) 罢了。
4. CIE 1931 标准中计算出的 Lʳ、Lᵍ 和 Lᵇ 分别为 1.000、4.5907 和 0.0601。这解释了维基百科的注解:
The resulting normalized color matching functions are then scaled in the
r : g : bratio of1 : 4.5907 : 0.0601for source luminance…
这句话的真正含义是,𝚽(𝛌)LʳR(𝛌)、𝚽(𝛌)LᵍG(𝛌) 和 𝚽(𝛌)LᵇB(𝛌) 表示匹配 𝚽(𝛌) 的亮度时红光、绿光和蓝光的亮度。
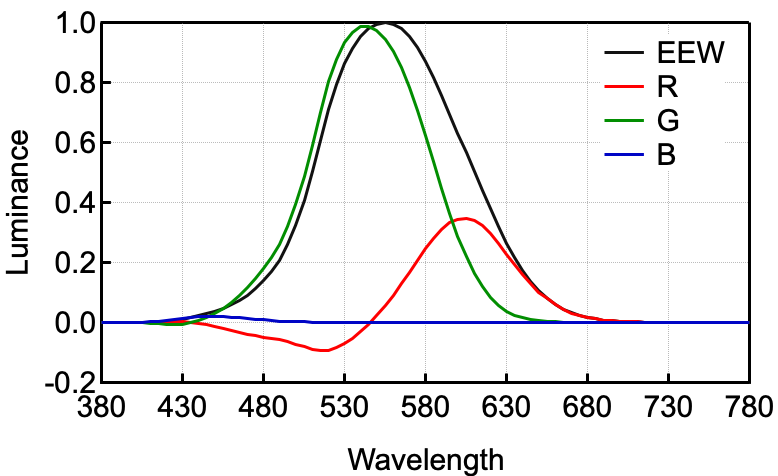
图 7:EEW 和三基色的亮度。
图 7 画出了 EEW 和三基色的亮度。不出所料,蓝光对亮度的贡献非常小,因为视网膜上 S 视锥细胞仅占约 2% 到 7% [Roorda 1999]。
5. 我们已经知道了 LʳR(𝛌)、LᵍG(𝛌) 和 LᵇB(𝛌) 表示匹配 1 W 的单色光 𝛌 的亮度时,所需红光、绿光和蓝光的亮度。那此时所需基色的功率呢?
红光的功率为 LʳR(𝛌)/V(700),即 R(𝛌) 乘以缩放因子 Lʳ/V(700)。同理,要计算绿光和蓝光的功率,G(𝛌) 和 B(𝛌) 分别乘以 Lᵍ/V(546.1) 和 Lᵇ/V(435.8)。三个缩放因子的比例为 Lʳ/V(700) : Lᵍ/V(546.1) : Lᵇ/V(435.8),归一化后即 72.0962 : 1.3791 : 1。
这解释了为什么维基百科说:
The resulting normalized color matching functions are then scaled in the
r : g : bratio of …72.0962 : 1.3791 : 1for source radiance.
其完整含义是,匹配 1 W 的单色光 𝛌 的亮度时,所需红光、绿光和蓝光的功率比例为 72.0962R(𝛌) : 1.3791G(𝛌) : B(𝛌)7。
6. 即便不知道亮度系数 Lʳ、Lᵍ 和 Lᵇ 的值,也有方法计算准确的数值。考虑到参考白光的三刺激值相等:
∫𝚽(𝛌)R(𝛌)d𝛌 = ∫𝚽(𝛌)G(𝛌)d𝛌 = ∫𝚽(𝛌)B(𝛌)d𝛌
如果 SPD 的采样点足够多,积分可以换成求和:
∑𝚽(𝛌)k(𝛌)r(𝛌) = ∑𝚽(𝛌)k(𝛌)g(𝛌) = ∑𝚽(𝛌)k(𝛌)g(𝛌)
代入 k(𝛌) = V(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌)) 得:
∑V(𝛌)𝚽(𝛌)r(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌)) =
∑V(𝛌)𝚽(𝛌)g(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌)) =
∑V(𝛌)𝚽(𝛌)b(𝛌) / (Lʳr(𝛌) + Lᵍg(𝛌) + Lᵇb(𝛌))
已知 V(𝛌), 𝚽(𝛌), r(𝛌), g(𝛌) 和 b(𝛌),有三个变量 Lʳ、Lᵍ、Lᵇ 和两个方程,因此可以解出变量间的比例。
观察 CIE RGB 数据向 CIE XYZ 变换的过程 [Fairman 1997] 发现,似乎 Lʳ、Lᵍ、Lᵇ 就是通过这种拟合方式算出来的,而不是用的 Wright-Guild 实验里被转换的数据。
6. 致谢
我非常想向 Arthur Broadbent 表达我的感激之情。他的逆向过程手法和对实验过程的详细记录就像魔法一样厉害。他在论文里使用的电子邮件地址 abroadbe@ubishops.ca 已经失效,非常希望能有人告诉我怎么联系他,以便我向他表示感谢!
参考
[Wright 1928] A re-determination of the trichromatic coefficients of the spectral colours. Trans Opt Soc London 1928–29;30:141–164
[Wright 1929] A re-determination of the mixture curves of the spectrum. Trans Opt Soc London 1929–30;31:201–211.
[Guild 1931] The colorimetric properties of the spectrum. Philos Trans Roy Soc London Ser. A 1931;230:149–187.
[Broadbent 2004a] A Critical Review of the Development of the CIE1931 RGB Color-Matching Functions. Color Research & Application 29(4):267–272. August 2004.
[Broadbent 2004b] Calculation from the original experimental data of the CIE 1931 RGB standard observer spectral chromaticity co-ordinates and color matching functions.
[Fairman 1997] Fairman HS, Brill MH, Hemmendinger H. How the CIE1931 color- matching functions were derived from the Wright–Guild data. Color Res Appl 1997;22:11–23.
[Service 2016] The Wright - Guild Experiments and the Development of the CIE 1931 RGB and XYZ Color Spaces.
[Roorda 1999] The arrangement of the three cone classes in the living human eye. Nature volume 397, pages 520–522(1999).
注释
-
这些数字并不精确,因为 CIE 1931 RGB CMF 是以 5 nm 的间隔发布的。我使用了最接近的值:G 对应 545 nm,B 对应 435 nm。如果需要更准确的数值,可以用高阶多项式来拟合 CMF,这也是色度学里的标准做法。 ↩︎
-
第二篇论文大概还没有正式发表,主要是第一篇的扩充版,不过第二篇叙述方式更加平易近人。 ↩︎
-
实践中这种关系取决于实验里旋钮的配置方式,可以是线性的、对数的,或者其它关系。理论上旋钮的读数如何反映放出的光的功率/亮度/光子数并不重要,只要我们能通过实验记录一个量到另一个量的映射关系即可。但由于光圈读数是光量的代理量,所以需要利用线性关系来应用 Grassmann 颜色线性律(Grassmann’s linear law of color)。 ↩︎
-
正如前面所提过的,需要假设光圈读数跟光功率是线性相关的,好让我们应用 Grassmann 颜色线性律。 ↩︎
-
实际上 Guild 1931 年论文里的值是
Lʳ = 1.0000, Lᵍ = 4.390, Lᵇ = 0.048。Broadbent 发现 Guild 当时犯了错,后来又订正了,但 Guild 从未公开发表过正确的结果。Broadbent [Broadbent 2004a, Broadbent 2004b] 根据 CIE 1931 RGB 数据逆向工程出了正确的值,也就是博文中列出的那三个。 ↩︎ -
此处同样是 Braodbent 修正后的结果。 ↩︎
-
给定面积和立体角时,功率之比跟辐亮度(radiance)之比是相等的。 ↩︎