前言

1920 年代末 Wright 和 Guild 的颜色匹配实验发展出了用红绿蓝三基色（primaries）定量表示所有人眼可见颜色的 CIE RGB 色彩空间，1931 年国际照明委员会（CIE）通过对 CIE RGB 色彩空间做线性变换得到了 CIE XYZ 色彩空间。XYZ 空间里的人眼可见色域（gamut of human vision）是一块从原点出发，向无限远处不断延伸的立体区域。将这块区域投影到 $X + Y + Z = 1$ 的平面上，就能画出方便展示的 CIE 1931 色度图（chromaticity diagram）（图自 维基）：

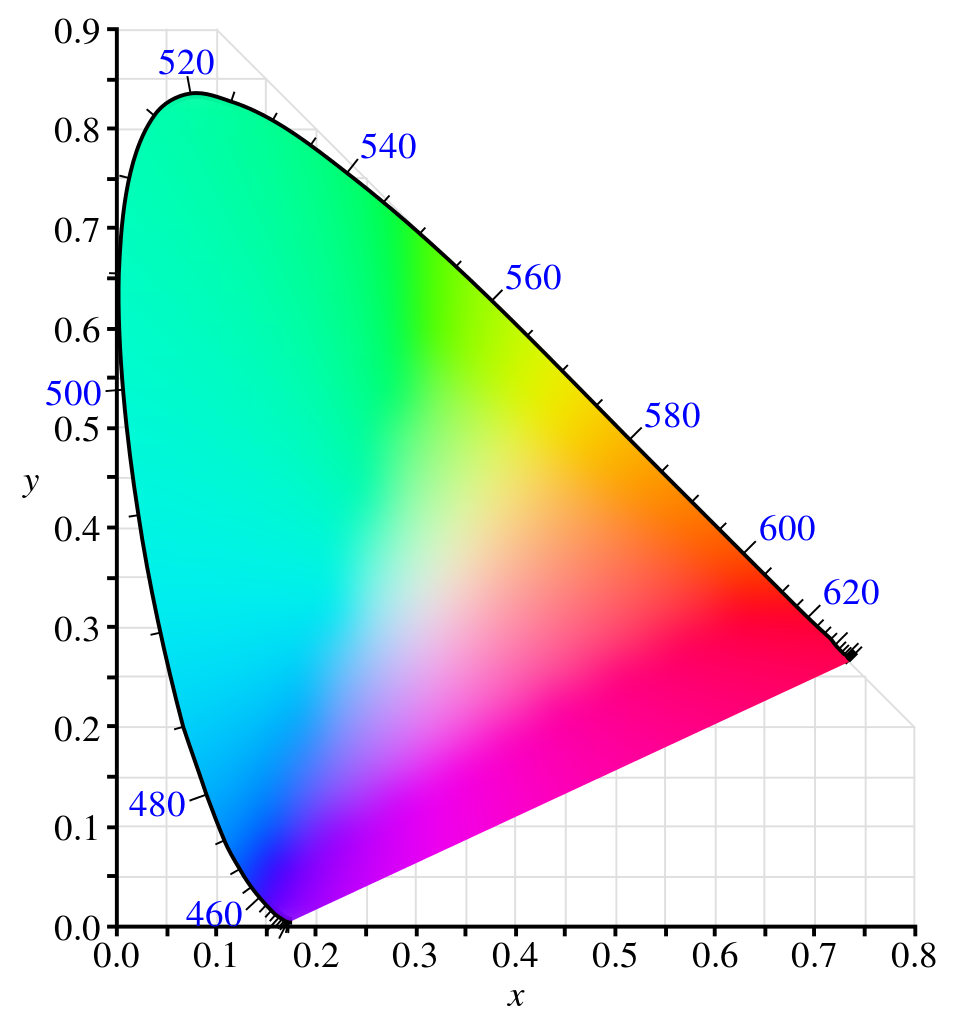
图中彩色马蹄形（horseshoe）的边界对应于单色光的颜色，并标出了波长的刻度；马蹄形内部则是单色光混合产生的颜色。解释一下色度图的横纵坐标：XYZ 空间可以理解为选取了三个假想色（imaginary colors）作为色彩空间里的基向量，使人眼可见色域恰好落入 XYZ 空间的第一卦限。混合颜色 $\boldsymbol{C}$ 需要 $(X, Y, Z)$ 份的假想色，将这些份数用总和归一化为比值，前两个比值就是色度图的坐标。

这张图在色彩科学教程中经常出现，不过日常里见得最多的场合估计还是电脑显示器的广告：显示器的每个像素由 RGB 子像素组成，依据三基色理论可以混合出任意颜色。但由于现实世界的功率不能为负数，所以三基色只能在色度图上圈出一个三角形的区域，对应于显示器所能产生的所有色度的颜色。广告里通常会给色度图叠上 sRGB 和 NTSC 的色域三角形，然后强调显示器能做到 100% 覆盖 sRGB 色域。

我想动手画一张色度图试试，通过实践加深对色彩的理解，本文的目的便是总结相关经验。另外我在网上搜索时发现除了 一篇用 Qt C++ 的博文，其它教程都是直接调用 python 的 Colour 包，或 Matlab 和 Mathematica 的内置函数来画的。所以本文也想填补 Python 从零实现的空白。

本文用到的 Python 包是 NumPy、Pandas 和 Matplotlib。完整代码和用到的数据可见 我的 Github 仓库。

画图思路

1. 在 xy 平面上用 np.linspace 和 np.meshgrid 构造网格。
2. 计算每个网格点的坐标 $(x, y)$ 对应的 sRGB。
3. 用 imshow 将网格当作彩色图片画出来。
4. 读取 XYZ 颜色匹配函数的色度坐标，构造马蹄形的 Polygon 去裁剪 imshow 的结果。
5. 在马蹄图边缘添加波长刻度。

思路不复杂，但坑却比想象中多，后面将会一一道来。

准备数据

在伦敦大学学院的 CVRL 实验室官网 下载：

• CIE 1931 2-deg, XYZ CMFs
• CIE 1931 2-deg xyz chromaticity coordinates

第一样是 CIE 1931 XYZ 颜色匹配函数（Color Matching Function, CMF），第二样是 CMF 的色度坐标，范围从 360 到 830 nm，分辨率为 1nm。

构造网格

人眼可见色域落在 xy 平面上的 $x,y \in [0, 1]$ 范围内，所以网格只需要在 $[0, 1]$ 之间取：

import numpy as np

N = 256
x = np.linspace(0, 1, N)
y = np.linspace(0, 1, N).clip(1e-3, 1)
x, y = np.meshgrid(x, y)

得到形如 (N, N) 的 xy 网格。如果 y 里含有 0，那么后续计算 Y / y 时将会出现除零警告，所以这里设置 y 的下限为 1e-3。

计算 sRGB

xyz 转换 XYZ

$(x, y)$ 坐标只表示颜色的色度，还要补上亮度（luminance） $Y$，将其转换为三刺激值（tristimulus） $(X, Y, Z)$ 后才能进一步变换为 RGB。

色度坐标的定义为

$$ \begin{align*} x &= \frac{X}{X + Y + Z} \cr y &= \frac{Y}{X + Y + Z} \cr z &= \frac{Z}{X + Y + Z} \end{align*} $$

假设已知亮度 $Y$，那么由定义可以推出 $X$ 和 $Z$

$$ \begin{align*} X &= x \frac{Y}{y} \cr Z &= (1 - x - y) \frac{Y}{y} \end{align*} $$

色度图里颜色的亮度可以随意指定，这里不妨设 $Y = 1$。代码如下：

Y = np.ones_like(y)
Y_y = Y / y
X = x * Y_y
Z = (1 - x - y) * Y_y
XYZ = np.dstack((X, Y, Z))

XYZ 转 sRGB

sRGB 是微软和惠普于 1996 年联合开发的用于显示器、打印机和互联网的色彩空间标准，s 意指 standard。PC 和互联网默认以 sRGB 标准解读图片存储的 RGB 数组，Matplotlib 也不例外。所以为了用 Matplotlib 绘制色度图，需要将 XYZ 坐标变换为 sRGB 坐标。sRGB 空间由 XYZ 空间线性变换而来，首先是在 XYZ 空间里选取新的红绿蓝三基色和白点

$$ \begin{align*} (x_r, y_r, z_r) &= (0.64, 0.33, 0.03) \cr (x_g, y_g, z_g) &= (0.30, 0.60, 0.10) \cr (x_b, y_b, z_b) &= (0.15, 0.06, 0.79) \cr (X_w, Y_w, Z_w) &= (0.95046, 1.0, 1.08906) \end{align*} $$

已知三基色的色度坐标，相当于知道了基向量的方向；已知白点的三刺激值，就可以确定基向量的长度，让 D65 白点在 RGB 空间里对应于 $(1, 1, 1)$。由此可以求得 XYZ 坐标到 sRGB 坐标的线性变换矩阵。具体求解过程可见 Computing RGB-XYZ conversion matrix，这里直接引用 维基 的结果

$$ \begin{bmatrix} R \cr G \cr B \end{bmatrix} = \begin{bmatrix} +3.2406 & -1.5372 & -0.4986 \cr -0.9689 & +1.8758 & +0.0415 \cr +0.0557 & -0.2040 & +1.0570 \end{bmatrix} \begin{bmatrix} X \cr Y \cr Z \end{bmatrix} $$

将变换矩阵记作 $\boldsymbol{M}$。前面得到的 XYZ 数组形如 (N, N, 3)，M 形如 (3, 3)，我们希望得到形如 (N, N, 3) 的 RGB 数组。按 NumPy 的矩阵乘法，我首先写出了：

RGB = M @ XYZ

这里 @ 运算符等价于 np.matmul。然而 NumPy 对多维数组矩阵乘法的处理是，让它最后两维都参与计算，所以会给出错误的结果。其实这种情况下更合适的算法是张量缩并（tensor contraction），设 XYZ 的元素为 $X_{ijk}$，RGB 的元素为 $C_{ijk}$，M 的元素为 $M_{ij}$，缩并公式为

$$ C_{ijk} = \sum_{l=1}^{3} X_{ijl} M_{kl} $$

这样计算出的 RGB 就是正确的。代码为：

M = np.array([
    [+3.2406, -1.5372, -0.4986],
    [-0.9689, +1.8758, +0.0415],
    [+0.0557, -0.2040, +1.0570]
])
RGB = np.tensordot(XYZ, M, (-1, 1))

别问什么是张量，问就是我也不会，这个矩阵乘法技巧是 stack overflow 上抄的。

sRGB 的定义要求 RGB 值在 $[0, 1]$ 范围内，即 RGB 空间里第一卦限内单位立方体的空间，超出范围的值我们可以用 np.clip 直接削头去尾：

RGB = RGB.clip(0, 1)

Gamma 校正

用 $\boldsymbol{M}$ 乘出来的 sRGB 还只是线性 sRGB，需要经过 gamma 校正后才能得到最后的结果。CRT 显示器的显示强度跟 RGB 像素值之间呈非线性关系

$$ I = A D^{\gamma} $$

其中 $I$ 是显示亮度，$A$ 是最大亮度，$D$ 是 $[0, 1]$ 之间的 RGB 像素值，一般有 $\gamma = 2.2$。下面画出函数 $y = x^{2.2}$ 的曲线：

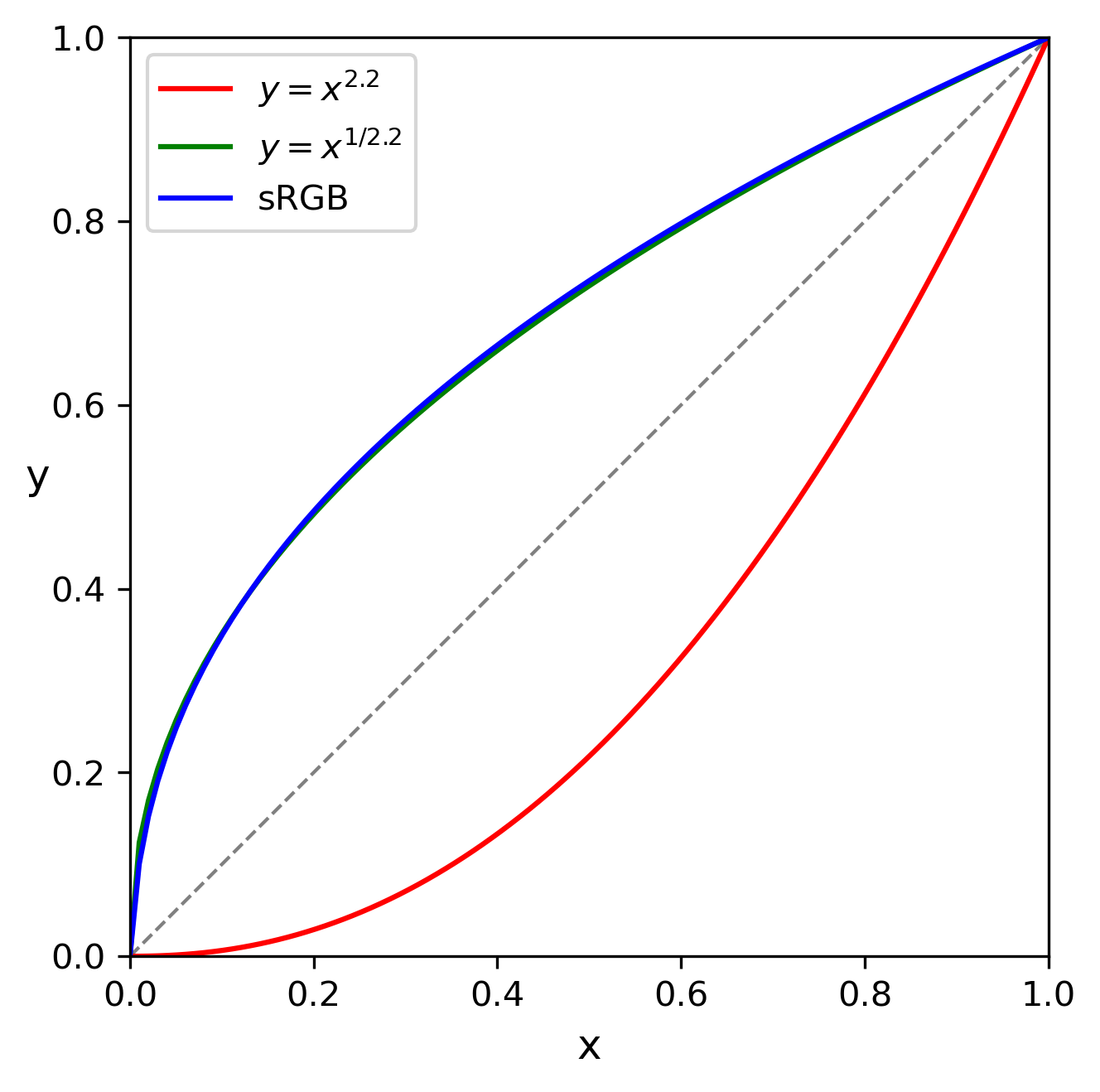
本来像素值跟颜色的亮度成线性关系，低像素值对应低亮度，但经过 CRT 显示器的非线性映射后，现在低像素值对应的亮度更低，并且在很大一段范围内都只能输出低亮度，只有当像素值接近于 1 时亮度才会陡然提升，这就会使图像显得更暗。为了修正这一问题，可以提前让 RGB 变为原来的 1/2.2 次方，这样经过 CRT 显示器的映射后就能变回原来的 RGB，显示正确的色彩。后来淘汰了 CRT 的液晶显示器并没有 $y = x^{2.2}$ 的非线性特征，但仍会通过电路模拟出这个效果，以正常显示 sRGB 标准的图像。上图的绿线画出了 $y = x^{1/2.2}$ 的曲线（几乎被蓝线挡住了），可以看到形状往上鼓，正好能抵消 $y = x^{2.2}$ 的下凹形状。

对线性的 sRGB 做 $y = x^{1/2.2}$ 映射的操作叫做 gamma 编码（encoding），反过来映射的操作就叫做 gamma 解码（decoding），gamma 校正就是指编码解码的这一过程。网上有文章认为 gamma 校正的深层原因是为了契合人眼对亮度的非线性感知，或者是先做 gamma 编码再做 8 bit 量化能保留更多暗部信息。相关讨论详见 色彩校正中的 gamma 值是什么？，这里不再深究。

sRGB 标准考虑到低亮度时的显示和量化误差等因素，设计出了跟 $y = x^{1/2.2}$ 非常接近，但存在细微区别的 gamma 编码方案

$$ C' = \begin{cases} 12.92 C \quad & C \le 0.0031308 \cr 1.055 C^{1/2.4} - 0.055 \quad & C \gt 0.0031308 \end{cases} $$

其中 $C$ 指代 $R$、$G$ 或 $B$。这一映射的曲线在上面的图中已用蓝线画出，与 $y = x^{1/2.2}$ 的曲线几乎重合。注意 $C \in [0, 1]$ 经过映射后仍有 $C' \in [0, 1]$。

经过 gamma 编码后的 RGB 值才是最终的 sRGB，代码如下：

# 使用np.where会遇到非正数求幂的问题.
mask = RGB > 0.0031308
RGB[~mask] *= 12.92
RGB[mask] = 1.055 * RGB[mask]**(1 / 2.4) - 0.055

色度图填色

绘制马蹄形轨迹

我将 CVRL 上下载的色度坐标数据更名为 cie_1931_2deg_xyz_cc.csv，用 Pandas 读取后构造 Matplotlib 的 Polygon 对象再添加到 Axes 上：

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon

fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.set_xlim(0, 0.8)
ax.set_ylim(0, 0.9)

cc = pd.read_csv('./data/cie_1931_2deg_xyz_cc.csv', index_col=0)
patch = Polygon(
    xy=cc[['x', 'y']],
    transform=ax.transData,
    ec='k', fc='none', lw=1
)
ax.add_patch(patch)

imshow 填色

imshow 能把形如 (M, N, 3) 的 RGB 数组当作彩色图片添加到 Axes 的指定位置上，imshow 的 clip_path 参数还能用 Polygon 的轮廓裁剪彩色图片，只保留落入 Polygon 内部的填色：

ax.imshow(
    RGB,
    origin='lower',
    extent=[0, 1, 0, 1],
    interpolation='bilinear',
    clip_path=patch
)

origin 和 extent 参数的用法请见 origin and extent in imshow。

亮度设置

前面的代码已经够画一张有模有样的色度图了，不过最大的坑也随之而来。下面展示 $Y = 1$ 和 $Y = 0.3$ 的结果：

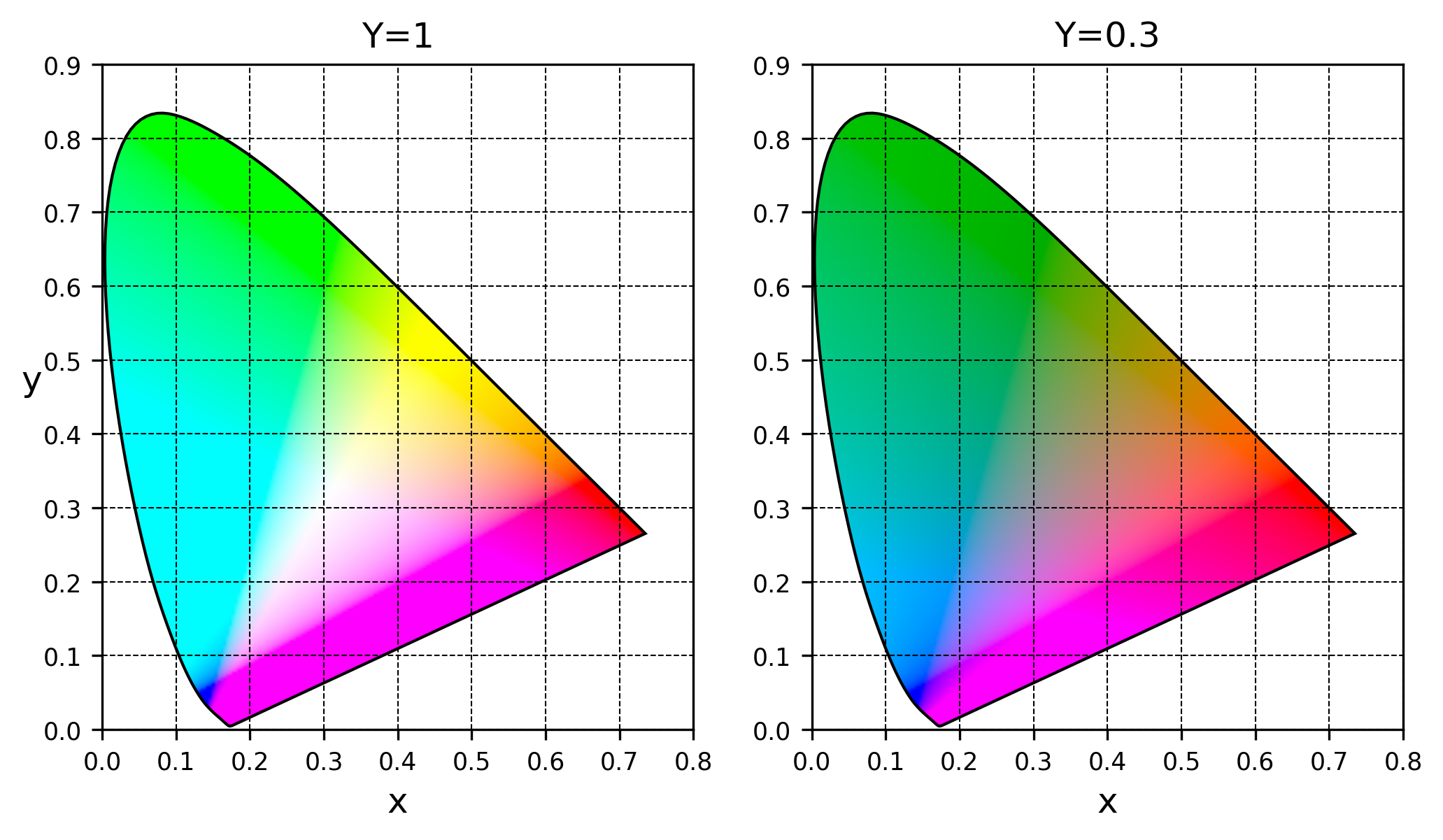
跟维基的效果很接近了，但却存在很大的违和感。首先 $Y = 1$ 时马蹄中心区域过白，令 $k = Y/y$，网格点的三刺激值为 $(kx, Y, k(1 - x - y))$，那么 $k$ 相当于 $x$ 和 $z$ 的放大因子。$Y = 1$ 时 $k$ 偏大，使马蹄中心的 RGB 值接近甚至超过 $(1, 1, 1)$，导致白了一片。

那么调低亮度使 $Y = 0.3$，马蹄中间不发白了，但和 $Y = 1$ 时一样，在紫红线上方仍有一大条紫色。考虑 XYZ 和 sRGB 的换算关系

$$ \begin{bmatrix} R \cr G \cr B \end{bmatrix} = \begin{bmatrix} +3.2406 & -1.5372 & -0.4986 \cr -0.9689 & +1.8758 & +0.0415 \cr +0.0557 & -0.2040 & +1.0570 \end{bmatrix} \begin{bmatrix} X \cr Y \cr Z \end{bmatrix} $$

紫红线附近 $k$ 大 $x$ 大，量级上有 $X > Z > Y$。观察变换矩阵 $\boldsymbol{M}$ 每一行的权重，可见第一行由正的 $X$ 主导，第二行由负的 $X$ 主导，第三行由正的 $Z$ 主导。因此紫红线附近的网格点 RGB 值大致满足 $R, B > 1$，$G < 0$，clip 后得 $(1, 0, 1)$，正好对应紫色。另外 clip 操作会通过削去高值降低 RGB 的量级，从而减小色度图部分区域的最终亮度。

进一步减小 $Y$ 能够隐去右下角的紫条，但也会使上方的颜色过于黯淡。因此考虑另外两种亮度设置：

1. $Y$ 随 $y$ 从 0 到 1 线性增大。
2. 任取正数 $Y$，先 clip 掉线性 sRGB 的负数分量，再除以 $C_{max} = \max \lbrace R, G, B \rbrace$，即用最大分量做归一化。

两种设置的效果如下图：

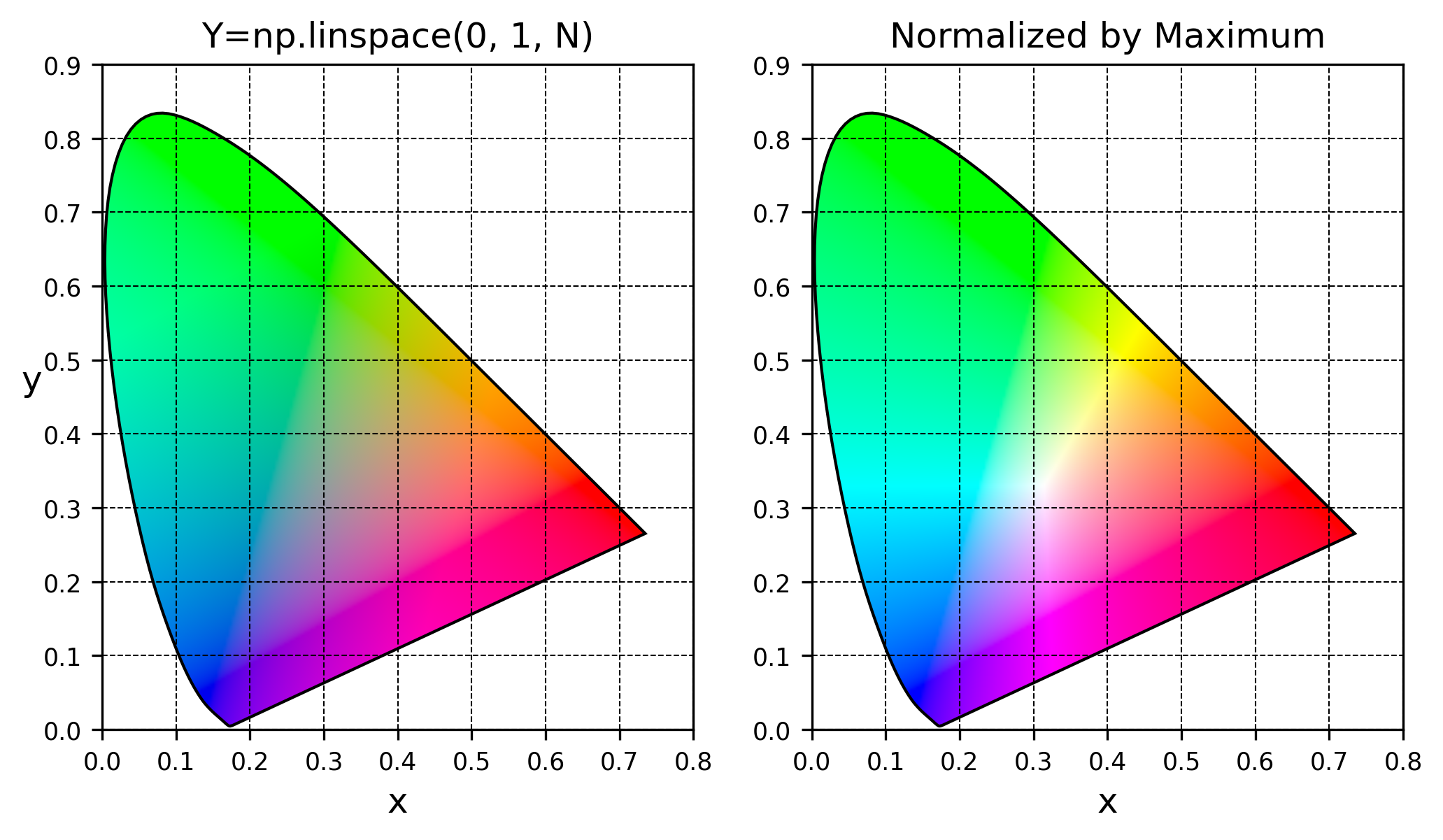
设置 1 的效果很不错，颜色过渡自然，红绿蓝紫青粉都有了；设置 2 的效果比 1 更明亮，但中间浮现出“Y”形亮纹。设置 2 里亮度任取，算出来的 RGB 无论是高是低，都会因为除以 $C_{max}$，使分量最高只有 1，这样一来就能在不需要用 clip 削头的情况下尽量提高每个网格点的亮度。至于亮纹，很容易推导出归一化后的亮度 $Y' = Y/C_m$，直觉告诉我 $R = G$、$R = B$、和 $G = B$ 时 $C_{max}$ 能取较小的值，将对应的三条直线投影到 $X + Y + Z = 1$ 平面上算出的直线确实跟“Y”形亮纹的位置重合，但你要问怎么证明我只能说不会。

设置 1 的代码为：

Y = np.linspace(0, 1, y.shape[0])
Y = np.broadcast_to(Y[:, np.newaxis], y.shape)
<计算sRGB和clip的代码>
<gamma encoding的代码>

设置 2 的代码为：

Y = np.ones_like(x)
<xyz转换XYZ的代码>
RGB = XYZ_to_sRGB(XYZ)
RGB = RGB.clip(0, None)
RGB /= RGB.max(axis=2, keepdims=True)
<gamma encoding的代码>

设置 2 的亮度表现跟维基图很接近了，但左上角部分发绿，而维基图则发青（cyan）。

色域出界处理

容易证明 XYZ 空间里两个颜色线性混合而成的颜色在色度图上正好落在两点间的连线上，所以 sRGB 三基色混合而成的颜色在色度图上对应于三基色围成的三角形区域，此即 sRGB 的色域。如果硬要用三基色混合出色域外的颜色，就会出现组合系数有负值的情况，RGB 表现为存在负数分量。前面我们的处理是简单粗暴地将负数分量修改为零（clip），这里介绍另一种处理方式：色度图上让色域外的颜色沿直线向白点移动，直至遇到三角形边界，用边界上的交点近似表示界外色。优点是能尽量维持界外色的色相（hue）。 设 $\boldsymbol{C_1}$ 为色域外的颜色，$\boldsymbol{C_2}$ 为 D65 白点

$$ \begin{align*} \boldsymbol{C_1} &= (R, G, B) \cr \boldsymbol{C_2} &= (1, 1, 1) \end{align*} $$

色域外要求 RGB 最小分量为负数

$$ C_{min} = \min \lbrace R, G, B \rbrace < 0 $$

色度图上让 $\boldsymbol{C_1}$ 向 $\boldsymbol{C_2}$ 移动相当于线性混合这两个颜色。不妨令混合色 $\boldsymbol{C_3} = \boldsymbol{C_1} + k\boldsymbol{C_2}$，比例系数 $k$ 使 $\boldsymbol{C_3}$ 的最小分量恰好为零，即 $\boldsymbol{C_3}$ 恰好落在三角形边界上。显然 $k = -C_{min}$，于是

$$ \begin{align*} \boldsymbol{C_3} &= \boldsymbol{C_1} + k\boldsymbol{C_2} \cr &= \boldsymbol{C_1} - C_{min} \boldsymbol{C_2} \cr &= (R - C_{min}, G - C_{min}, B - C_{min}) \cr \end{align*} $$

$\boldsymbol{C_3}$ 的最小分量为 $C_{min} - C_{min} = 0$。一句话概括该方法：如果一个颜色的最小分量为负数，那么让每个分量都减去这个负数。如此处理后分量可能超过 1，可以再应用上一节的设置 2，除以新的 $C_{max}$ 做归一化。跟 clip 处理的对比如下图：

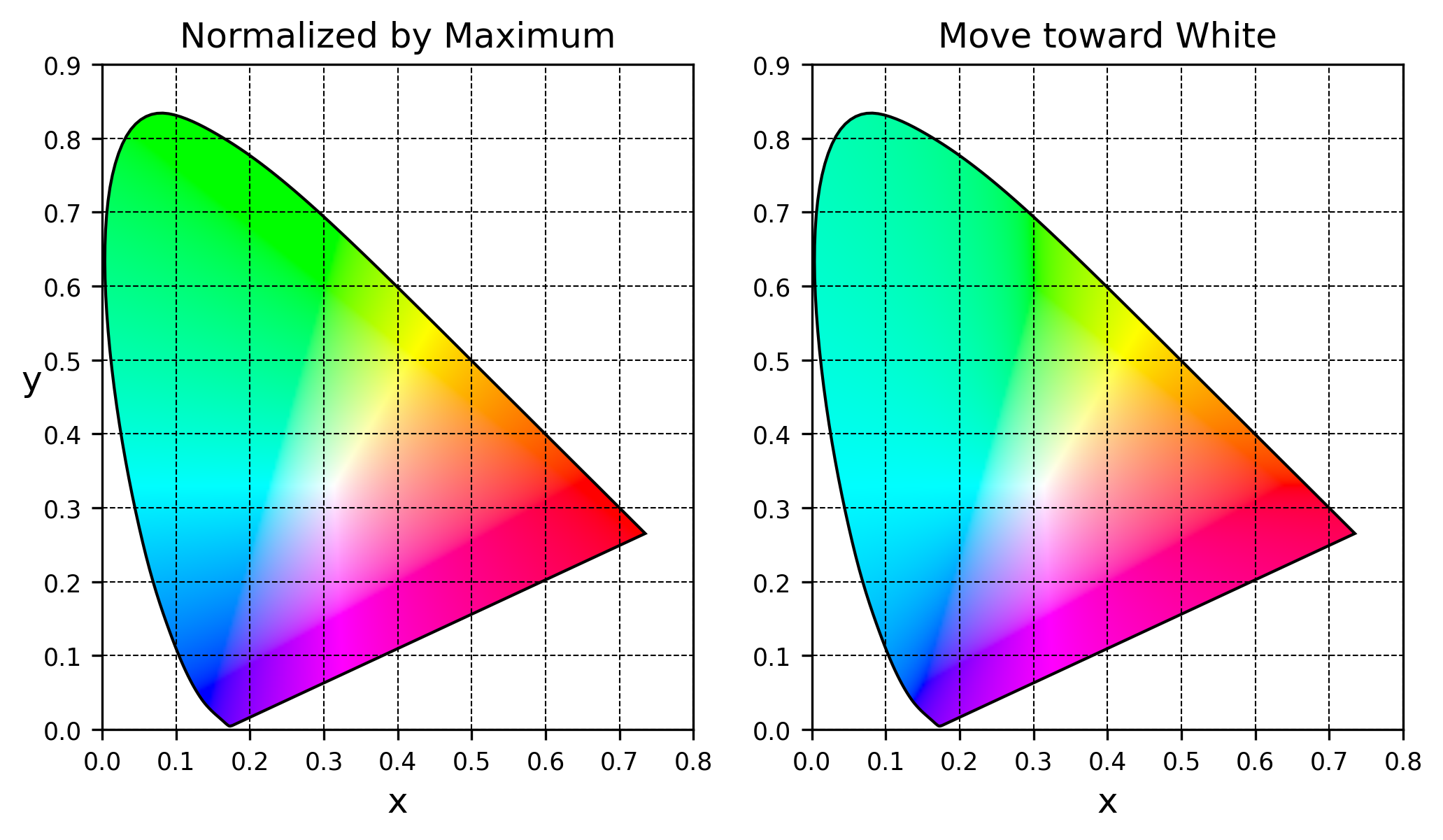
区别是左半区域显得更青，色彩跟维基的图几乎一致了。所以本文最后决定通过混合白色处理出界色，用最大分量做归一化设置亮度。如果读者不喜欢这种发青的效果，可以自行尝试不同的设置。

代码如下：

Y = np.ones_like(x)
<xyz转换XYZ的代码>
RGB = XYZ_to_sRGB(XYZ)
RGB -= RGB.min(axis=2, keepdims=True).clip(None, 0)
RGB /= RGB.max(axis=2, keepdims=True)
<gamma encoding的代码>

波长刻度

马蹄形边界一圈（不含紫红线）对应于单色光的颜色，维基的图中给边界标注了对应波长的刻度，可以看到从紫色到红色，波长从 460 nm 升至 620 nm。Matplotlib 只支持给 Axes 的四周标刻度，像这种曲线上的刻度我们只能自己用 plot 方法来画。以边界曲线上一点 $(x_i, y_i)$ 为例，刻度长度自定，如果已知该点的法向方向，就能根据刻度长度 $L$ 和方向确定刻度终点 $(x'_i, y'_i)$。求离散曲线的法向方向，网上有说直接用差分近似导数的，有说用三点共圆的，还有三次样条插值后再求导的。我参考的是论文 色度図の着色 里的做法，核心思路是对于相邻的三点 $P_1$、$P_2$ 和 $P_3$，以连线 $P_1 P_3$ 的垂线方向作为 $P_2$ 点的法向：

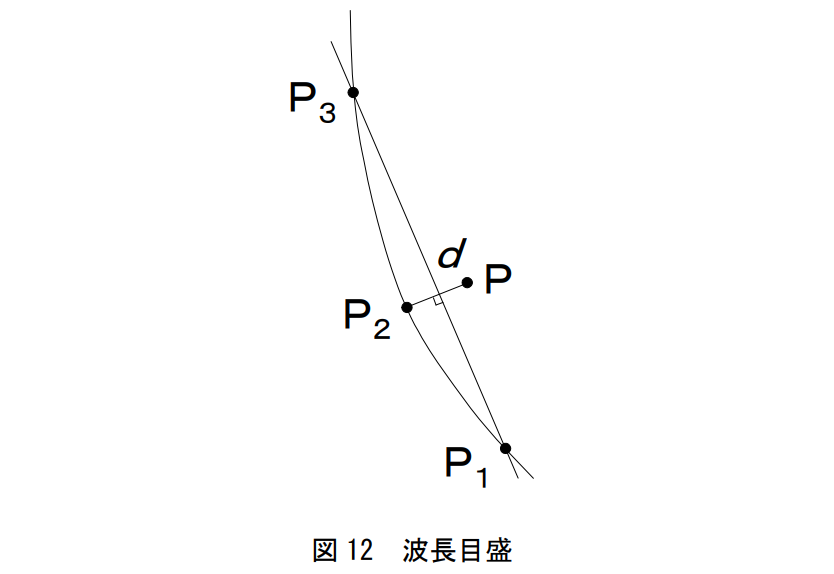
这个算法实现起来比较简单，并且可以向量化。计算公式为

$$ \begin{gather*} \Delta x_i = x_{i + 1} - x_{i - 1} \cr \Delta y_i = y_{i + 1} - y_{i - 1} \cr \Delta l_i = \sqrt{\Delta x_i^2 + \Delta y_i^2} \cr \cos \theta_i = -\Delta y_i / \Delta l_i \cr \sin \theta_i = \Delta x_i / \Delta l_i \cr x'_i = x_i + L \cos \theta_i \cr y'_i = y_i + L \sin \theta_i \end{gather*} $$

其中 $\theta_i$ 是法向跟 x 轴的夹角。代码为：

x, y = cc['x'], cc['y']
xy = np.column_stack((x, y))
dxdy = np.zeros_like(xy)
dxdy[0] = xy[1] - xy[0]
dxdy[-1] = xy[-1] - xy[-2]
dxdy[1:-1] = xy[2:] - xy[:-2]
dx, dy = dxdy[:, 0], dxdy[:, 1]
dl = np.hypot(dx, dy)
dl[dl <= 0] = np.nan
cos = -dy / dl
sin = dx / dl

cs = pd.DataFrame(
    data=np.column_stack((cos, sin)),
    index=cc.index,
    columns=['cos', 'sin']
)
cs.loc[(cs.index < 430) | (cs.index > 660)] = np.nan
cs = cs.ffill().bfill()
cos, sin = cs['cos'], cs['sin']

tick_len = 0.03
tick_df = pd.DataFrame({
    'x0': x,
    'y0': y,
    'x1': x + tick_len * cos,
    'y1': y + tick_len * sin,
})

ticks = [380, *range(460, 601, 10), 620, 700]
tick_df = tick_df.loc[ticks]
for row in tick_df.itertuples():
    ax.plot(
        [row.x0, row.x1],
        [row.y0, row.y1],
        c='k', lw=0.6
    )

中间用到了 DataFrame 能用标签进行索引的特性。这里还有一个隐藏的坑：波长很小时 CMF 的色度坐标不是很精准，放大后会看到曲线歪歪扭扭，因此算出的法向一会儿朝左一会儿朝下，并不稳定；波长很大时 $\Delta x_i$ 和 $\Delta y_i$ 全为零，无法计算夹角。这里将波长小于 430 nm 部分的 $\Delta x_i$ 和 $\Delta y_i$ 都修改成 430 nm 处的值，波长大于 660 nm 的部分同理。具体到代码是通过 Pandas 的 ffill 和 bfill 实现的。

给刻度加标签的操作类似，无非是将刻度长度拉长，计算出距离更远的 $(x'_i, y'_i)$，然后用 text 方法加字。

最终效果

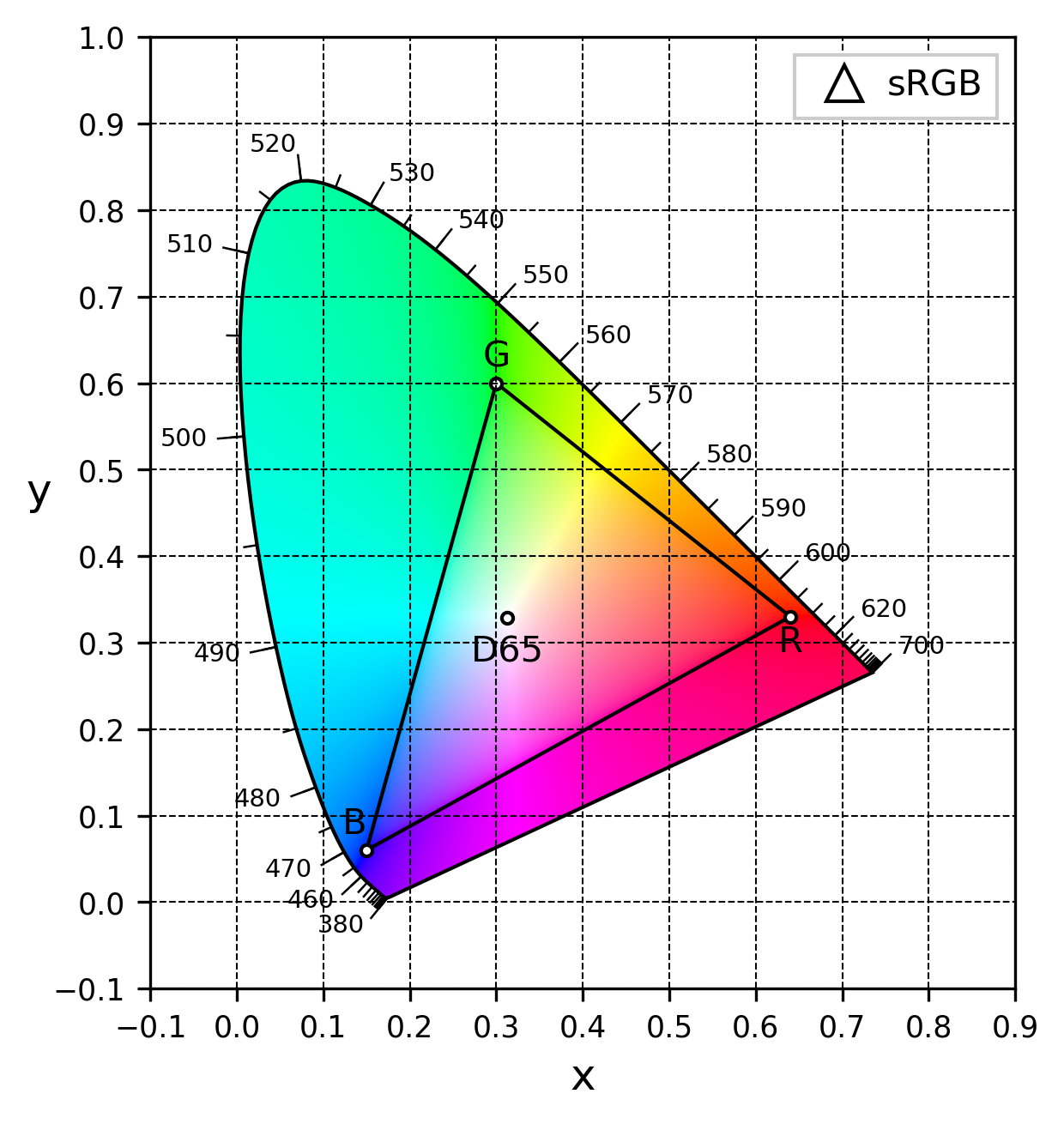
还额外画上了表示 sRGB 色域的三角形和 D65 白点。

最后再顺手实现一下基于 CIE RGB 空间的 rg 色度图。同样是在 rg 空间里拉出网格，将 rg 按比例放大为 RGB，计算 CIE RGB -> XYZ -> sRGB，其中 CIE RGB 到 XYZ 的变换公式为

$$ \begin{bmatrix} X \cr Y \cr Z \end{bmatrix} = \begin{bmatrix} 2.76888 & 1.75175 & 1.13016 \cr 1.00000 & 4.59070 & 0.06010 \cr 0.00000 & 0.05651 & 5.59427 \end{bmatrix} \begin{bmatrix} R \cr G \cr B \end{bmatrix} $$

这个公式还会用于将 XYZ CMF 变换为 RGB CMF，再归一化为色度坐标，用来画单色光轨迹和裁剪 imshow。最后额外画上 XYZ 空间三基色投影在 rg 平面上的三角形：

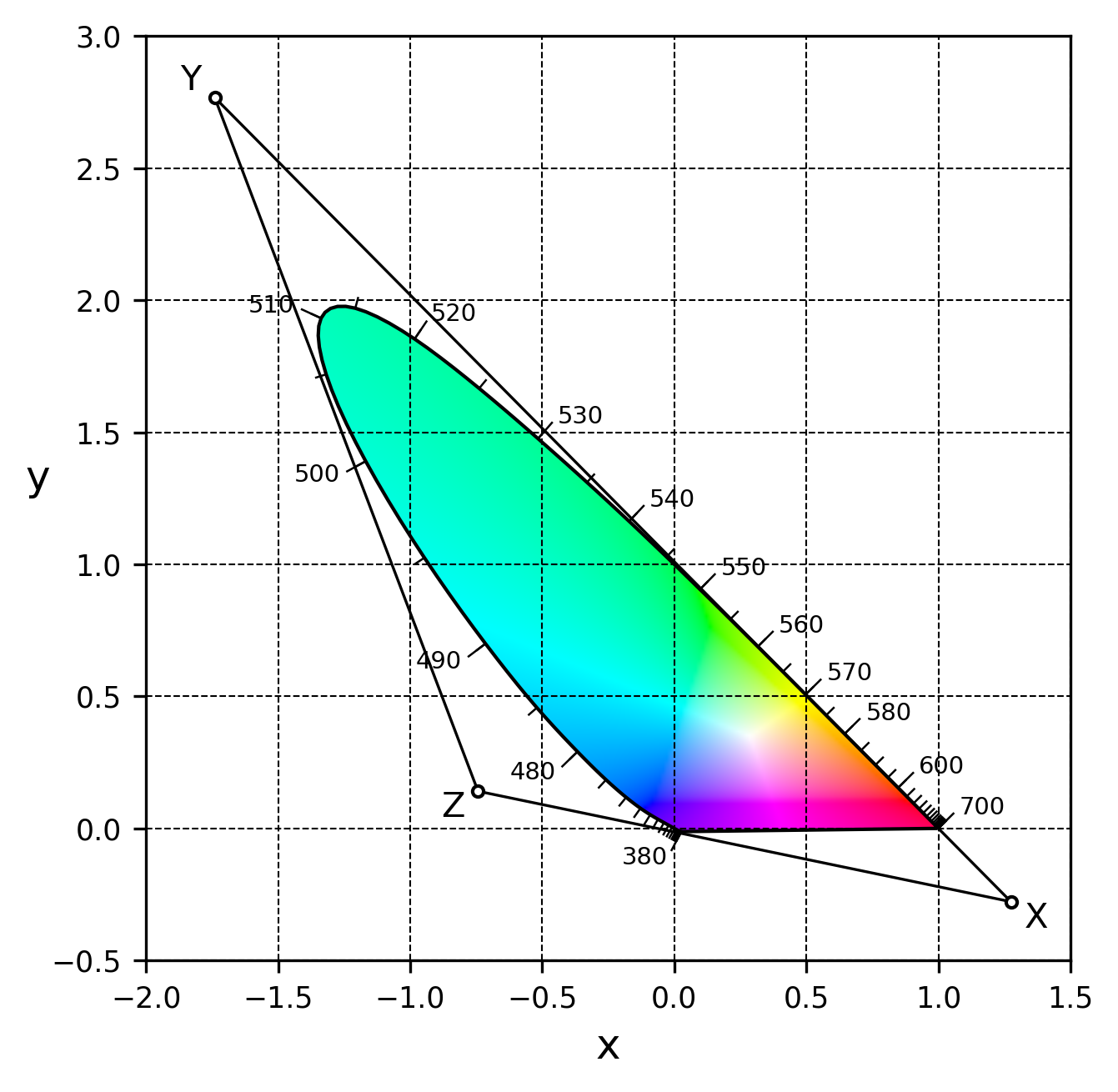
结语

至此已经成功复现了 CIE 1931 色度图，该过程充分考验了我们对 CIE RGB、XYZ 和 sRGB 空间的理解，也引入了一些 NumPy 和 Matplotlib 的使用技巧。不过本文的理解和实现也不一定正确，工作中还是更推荐调用 Colour 包的 plot_chromaticity_diagram_CIE1931 的函数，既方便又可靠。读者有问题还请多多指出。

参考资料

Color Vision and Colorimetry: Theory and Applications, Second Edition

Wikipedia: CIE 1931 color space

Wikipedia: sRGB

Proposal for a Standard Default Color Space for the Internet—sRGB

Color space conversion (2) RGB-XYZ conversion

Rendering Spectra

色度図の着色

如何绘制CIE1931xy色度图