Cartopy 系列：利用多边形生成掩膜数组

二维平面上一系列点的坐标由 x 和 y 数组描述，同时准备一个形状相同的 mask 数组。若第 i 个点落入了平面上一个多边形的内部，则令 mask[i] = True；若在多边形外，则令 mask[i] = False。由此得到的 mask 数组即掩膜（mask）数组，它可以作为布尔索引分出多边形内外的点

x_in, y_in = x[mask], y[mask]
x_out, y_out = x[mask], y[mask]

它可以作为掩膜，掩盖多边形范围外的值——即把外面的值设为 NaN，以便进行后续的计算

z[~mask] = np.nan
z_mean = np.nanmean(z)

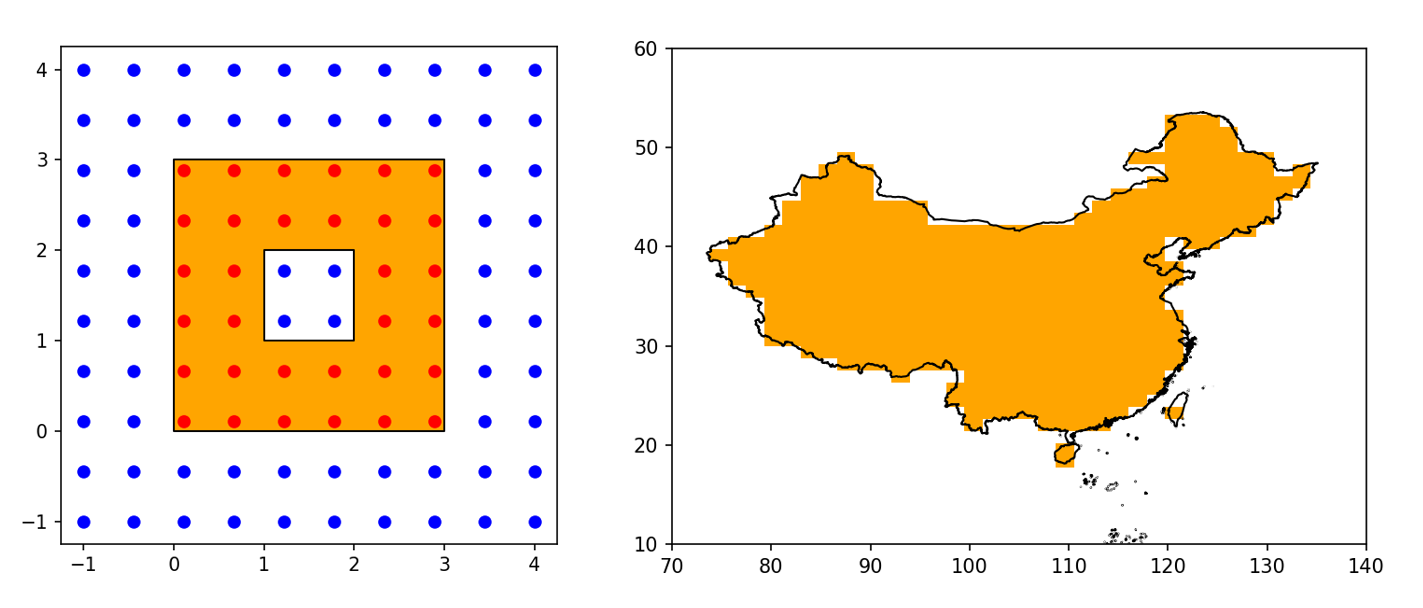
下图展示了两个应用：左小图的多边形是一个中心带洞的正方形，给定一系列散点的坐标，计算出掩膜后可以把多边形内的散点画成红色，多边形外的散点画成蓝色；右小图的多边形是中国全域，给定 (50, 50) 形状的经纬度网格，计算出掩膜后用橙色画出掩膜为 True 的部分，这张掩膜之后可以用来处理网格上的其它变量。

diagram

本文的目的是介绍如何用 Python 制作掩膜数组，并尽量优化其运行时间。从 shapefile 中读取中国国界并转化为 Shapely 中的多边形对象等操作，已经在博文 Cartopy 系列：探索 shapefile 中详细介绍过了，本文是对其的一个补充。

基本思路

首先准备多边形和测试用的坐标点。多边形使用中国国界，通过 cnmaps 包的 get_adm_maps 函数获取

from cnmaps import get_adm_maps

china = get_adm_maps(level='国', record='first', only_polygon=True)

由此得到的 china 是 MapPolygon 对象，继承自 Shapely 的 MultiPolygon 对象，即中国由很多个多边形组成（大陆和海岛）。MultiPolygon.contains 方法可以用来检查另一个 Shapely 的几何对象是否被多边形所包含。对于坐标点来说，要求点落入多边形内部，恰好落在多边形的边界上并不算数。

坐标点选用覆盖中国范围的网格

import numpy as np

lonmin, lonmax = 60, 150
latmin, latmax = 0, 60
npt = 50
x = np.linspace(lonmin, lonmax, npt)
y = np.linspace(latmin, latmax, npt)
x, y = np.meshgrid(x, y)

生成掩膜数组的思路非常简单：循环遍历 x 和 y，每个点对应一个 Shapely 的 Point 对象，调用 MultiPolygon.contains 方法检查点是否落入多边形中，最后返回收集好的结果。代码如下

import shapely.geometry as sgeom

def polygon_to_mask(polygon, x, y):
    '''生成落入多边形的点的掩膜数组.'''
    x = np.atleast_1d(x)
    y = np.atleast_1d(y)
    mask = np.zeros(x.shape, dtype=bool)

    # 判断每个点是否落入polygon, 不包含边界.
    for index in np.ndindex(x.shape):
        point = sgeom.Point(x[index], y[index])
        if polygon.contains(point):
            mask[index] = True

    return mask

其中 np.ndindex 是用来遍历多维数组的迭代器类，简单理解一下就是用了它就可以少写多重循环。使用方法很简单

mask = polygon_to_mask(china, x, y)

计时发现，该函数对单个点需要 57 毫秒，对 10 * 10 = 100 个点需要 3 秒，对 50 * 50 = 2500 个点需要 88 秒。显然这个速度太慢了，假设耗时与点数成线性增长关系，对于 70° - 140°E，10° - 60°N，分辨率为 0.25° 的 ERA5 格点数据，恐怕要跑 50 分钟以上。结论是，当点数只有几十个时 polygon_to_mask 还能用用，几百个点以上时该函数基本没有实用价值。

利用 shapely.prepared.prep 进行优化

在翻阅 Shapely 的文档时我注意到了 Prepared Geometry Operations 一节，提到使用 shapely.prepared.prep 函数将几何对象转为“准备好了”（prepared）的对象后，能加速 contains 和 intersects 等方法的批处理。于是 polygon_to_mask 有了第二个版本

from shapely.prepared import prep

def polygon_to_mask(polygon, x, y):
    '''生成落入多边形的点的掩膜数组.'''
    x = np.atleast_1d(x)
    y = np.atleast_1d(y)
    mask = np.zeros(x.shape, dtype=bool)

    # 判断每个点是否落入polygon, 不包含边界.
    prepared = prep(polygon)
    for index in np.ndindex(x.shape):
        point = sgeom.Point(x[index], y[index])
        if prepared.contains(point):
            mask[index] = True

    return mask

相比第一个版本，函数体几乎只有一行的改动。这次单个点耗时 14 毫秒，10 * 10 = 100 个点耗时 0.02 秒，50 * 50 = 2500 个点耗时 0.06 秒。速度可以说提升了两到三个数量级，作为 Python 函数来说终于有了实用性。不过对于 1000 * 1000 = 1e6 个点还有些吃力，需要 10 秒。

利用递归分割进行优化

在找到 prepared 模块前我曾在 Github Gist 上看到了 perrette 设计的 shp_mask 函数，他的思路是：

先确定坐标点的边界框（形如 (xmin, xmax, ymin, ymax) 的矩形区域）。
如果边界框在多边形外，这些坐标点对应的掩膜直接设为 False。
如果边界框被多边形包含，这些坐标点对应的掩膜直接设为 True。
如果边界框与多边形相交，将边界框等分成四个子区域，对每个子区域递归应用上面的流程。
如果某层递归只传入了单个点，直接返回多边形与这个点的包含关系。

于是我想能不能借鉴递归分割的思路，同时加上 prepared 的加速效果。shp_mask 函数接受的 x 和 y 要求是张成网格的一维坐标，不过我希望 polygon_to_mask 接受的 x 和 y 不一定非得是网格坐标，无序摆放的散点也可以。按这个要求修改后得到第三个版本

import math

def polygon_to_mask(polygon, x, y):
    '''生成落入多边形的点的掩膜数组.'''
    x = np.atleast_1d(x)
    y = np.atleast_1d(y)
    if x.shape != y.shape:
        raise ValueError('x和y的形状不匹配')
    prepared = prep(polygon)

    def recursion(x, y):
        '''递归判断坐标为x和y的点集是否落入多边形中.'''
        xmin, xmax = x.min(), x.max()
        ymin, ymax = y.min(), y.max()
        xflag = math.isclose(xmin, xmax)
        yflag = math.isclose(ymin, ymax)
        mask = np.zeros(x.shape, dtype=bool)

        # 散点重合为单点的情况.
        if xflag and yflag:
            point = sgeom.Point(xmin, ymin)
            if prepared.contains(point):
                mask[:] = True
            else:
                mask[:] = False
            return mask

        xmid = (xmin + xmax) / 2
        ymid = (ymin + ymax) / 2

        # 散点落在水平和垂直直线上的情况.
        if xflag or yflag:
            line = sgeom.LineString([(xmin, ymin), (xmax, ymax)])
            if prepared.contains(line):
                mask[:] = True
            elif prepared.intersects(line):
                if xflag:
                    m1 = (y >= ymin) & (y <= ymid)
                    m2 = (y >= ymid) & (y <= ymax)
                if yflag:
                    m1 = (x >= xmin) & (x <= xmid)
                    m2 = (x >= xmid) & (x <= xmax)
                if m1.any(): mask[m1] = recursion(x[m1], y[m1])
                if m2.any(): mask[m2] = recursion(x[m2], y[m2])
            else:
                mask[:] = False
            return mask

        # 散点可以张成矩形的情况.
        box = sgeom.box(xmin, ymin, xmax, ymax)
        if prepared.contains(box):
            mask[:] = True
        elif prepared.intersects(box):
            m1 = (x >= xmid) & (x <= xmax) & (y >= ymid) & (y <= ymax)
            m2 = (x >= xmin) & (x <= xmid) & (y >= ymid) & (y <= ymax)
            m3 = (x >= xmin) & (x <= xmid) & (y >= ymin) & (y <= ymid)
            m4 = (x >= xmid) & (x <= xmax) & (y >= ymin) & (y <= ymid)
            if m1.any(): mask[m1] = recursion(x[m1], y[m1])
            if m2.any(): mask[m2] = recursion(x[m2], y[m2])
            if m3.any(): mask[m3] = recursion(x[m3], y[m3])
            if m4.any(): mask[m4] = recursion(x[m4], y[m4])
        else:
            mask[:] = False

        return mask

    return recursion(x, y)

运行时间如下图所示

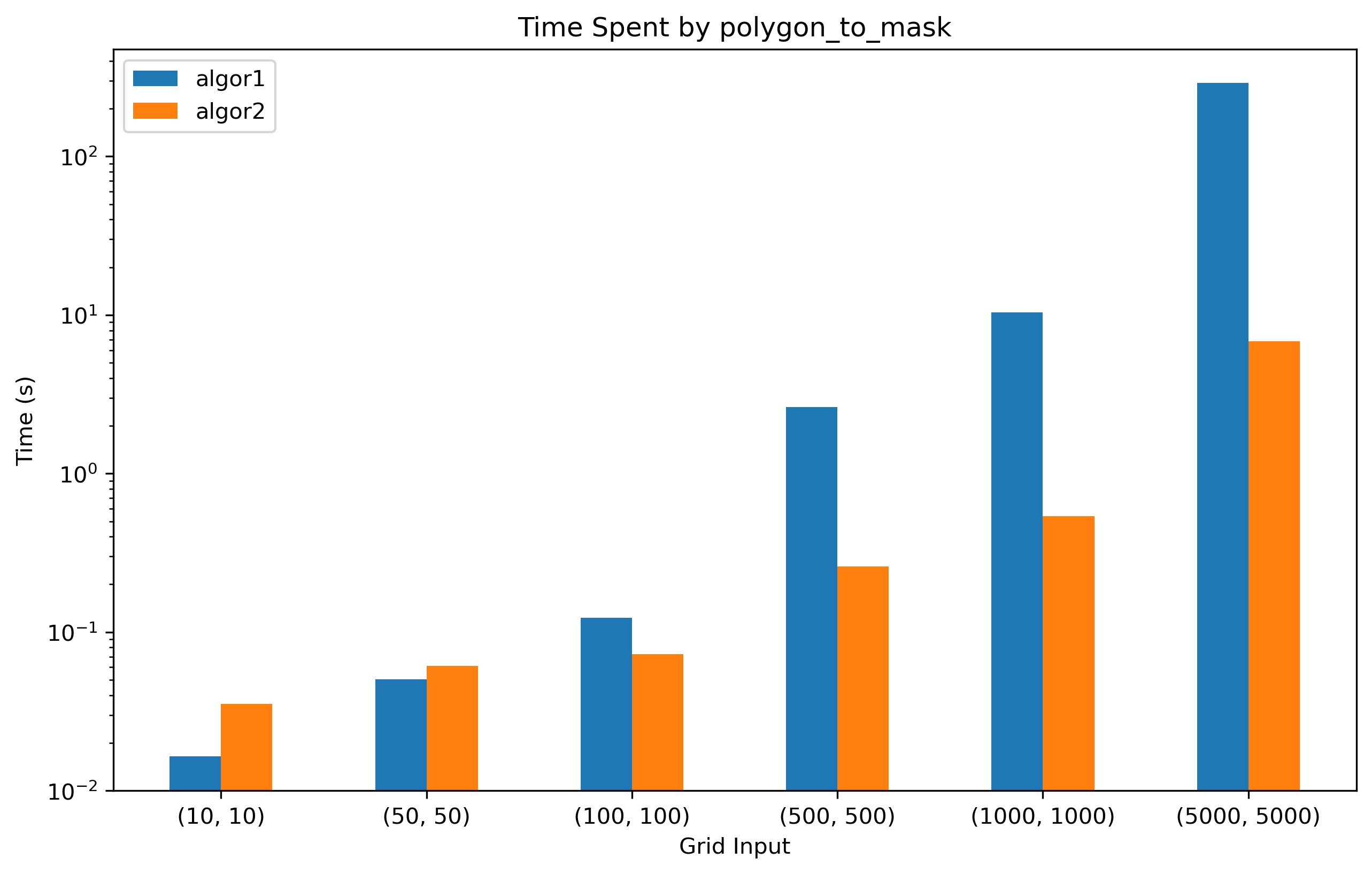
timing

蓝色柱状图对应于加了 prepared 的循环版，橙色柱状图对应于递归版。当点数小于 50 * 50 = 2500 时，递归版反而更慢；而当点数达到 1e5 量级时，递归版的优势就非常显著了。例如对于 (1000, 1000) 的输入，循环版耗时 10.4 秒，递归版耗时 0.5 秒；对于 (5000, 5000) 的输入，循环版耗时 290.5 秒，递归版耗时 6.8 秒。不过我还没看内存占用的差异，估计递归所需的内存会高一些，感兴趣的读者可以用 memory_profiler 包测试一下。

总结

对于 (1000, 1000) 形状的输入，我们通过优化，使 polygon_to_mask 函数的耗时从 57000 秒（理论上）缩短到 10 秒，再缩短到 0.5 秒，一共加快约 114514 倍，可以说非常惊人了。不过我觉得可能还有优化的余地，例如对于 MultiPolygon，可以先计算每个成员 Polygon 的掩膜数组，收集起来叠加成 masks 数组，最后通过 mask = np.any(masks, axis=0) 合并掩膜。当然追求极致效率的读者可以了解一下 GDAL 库里的 gdal_rasterize 命令。